Software: SimX - Einfuehrung - Elektro-Chaos - Schwingkreis mit C-Diode

↑

← →

Nichtlinearer Schwingkreis mit C-Diode (Chaos-Experimente)

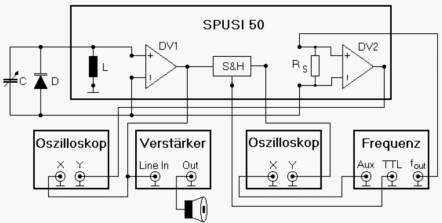
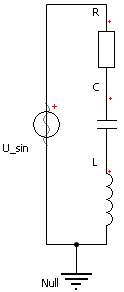
Nach einigen theoretischen Betrachtungen soll versucht werden, reale physikalische Chaos-Experimente mittels der numerischen Simulation nachzuvollziehen. Dabei benutzen wir die Veröffentlichung Experimente zur Untersuchung linearer und nichtlinearer elektrischer Serienschwingkreise von Burkhard Wolf und Hans-Josef Patt, welche als PDF-Datei abrufbar ist. Die Kapazitätsdiode wird hier als Bestandteil eines Serienschwingkreises benutzt. Das folgende Bild aus der PDF-Datei zeigt die Original-Schaltung:

Nichtlineare Systeme

Alle Systeme, welche nicht als lineare Systeme behandelt werden können, sind nichtlineare Systeme:

• Nichtlineare Systeme enthalten Elemente, deren Parameterwerte abhängig von der Belastung des Elements sind (z.B. Kapazität als Funktion der anliegenden Spannung) oder erhalten "zufällige" Eingangssignale (z.B. zeitabhängige Frequenzänderung der Betriebsspannung).
• Für nichtlineare Systeme existieren (im Normalfall) keine analytischen Lösungen.
• Nichtlinearität ist in Natur und Technik der Regelfall. Die linearen Näherungen der klassischen Natur- und Technikwissenschaften beschreiben nur die grundlegenden Effekte (kausalen Zusammenhänge) der jeweiligen physikalisch-technischen Domäne (E-Technik, Mechanik, Fluidtechnik, usw.). Sie vermitteln damit das grundlegende Verständnis, welches man auch zur Modellierung nichtlinearer Systeme anwenden kann.
• Das Verhalten nichtlinearer Systeme kann der "gesunde Menschenverstand" nicht immer vorhersagen. Ähnliche Startbedingungen führen häufig zu stark verändertem Verhalten.

Chaotische Systeme

Damit ein nichtlineares System chaotisches Verhalten zeigt, müssen zusätzlich zur "Nichtlinearität" weitere Kriterien erfüllt sein:

• Es muss mindestens eine Stelle starker sensitiver Abhängigkeit von den Anfangsbedingungen existieren. Umgangssprachlich ist dies als Schmetterlingseffekt bekannt. Kleinste Änderungen der Startparameter führen langfristig zu völlig anderem Verhalten. Man spricht hierbei von deterministischem Chaos.
• Das System muss hinreichend viele Freiheitsgrade für die Bewegung im sogenannten Phasenraum besitzen:
  • Der Zustand eines Systems wird zu jedem Zeitpunkt durch einen Punkt in einem Raum dargestellt werden, dessen Koordinatenachsen durch den Satz der unabhängigen Zustandsgrößen (meist Integralgrößen) des Systems gegeben sind. Die Dynamik des Systems lässt sich damit als Bahn (Trajektorie) dieses Punktes im Phasenraum interpretieren. So wird beispielsweise der Phasenraum eines LCR-Schwingkreises durch den Spulenstrom und die Kondensatorspannung aufgespannt. Die ungedämpfte Schwingung entspricht einer geschlossenen Kurve um den Koordinatenursprung.
  • Die Trajektorie eines Systems kann sich innerhalb des Phasenraums nicht schneiden, weil dies der Eindeutigkeit der Systementwicklung ausgehend von einem Punkt im Phasenraum widersprechen würde. In der Ebene kann es deshalb nur zu spiralähnlichen Kurven kommen. Als Spezialfall ist für ungedämpft oszillierende Systeme die geschlossene Trajektorie möglich.
  • Erst durch einen zusätzlichen Freiheitsgrad ist es im Beispiel des LCR-Schwingkreises möglich, dass von der Spiralform abweichende Trajektorien entstehen, weil "Schnittpunkte" durch Ausweichen in der 3. Koordinatenachse vermieden werden können. Der zusätzliche Freiheitsgrad wird durch die äußere Anregung des Schwingkreises mit einer zeitveränderlicher Spannung geschaffen.
• Eine maßvolle Dämpfung muss für eine dosierte Energieabfuhr sorgen, damit das System weder "explodiert" noch "erstarrt".

Der Phasenraum eines Reihenschwingkreises

Ein LCR-Schwingkreis besitzt zwei Energiespeicher mit jeweils einer energetischen Zustandsgröße (Spulenstrom und Kondensatorspannung):

• Der Wert einer energetischen Zustandsgröße beschreibt eindeutig die aktuell im zugehörigen Speicher enthaltene Energiemenge.
• Ausgehend von einem gegebenen Ladezustand der Energiespeicher entwickelt sich das System determiniert im Zeitbereich, weil zwischen den Speichern ein Energiefluss über die vorhandenen Verbindungselemente erfolgt.
• Die Entwicklung eines Systems in der Zeit wird durch die aktuellen Werte aller Zustandsgrößen eindeutig beschrieben.
• Sehr anschaulich sieht man die Systementwicklung durch die Trajektorie des Systemzustands im Phasenraum.
• Beim schrittweisen Aufbau des Chaos-Experiments werden wir den Phasenraum detailliert betrachten.

Linearer Schwingkreis

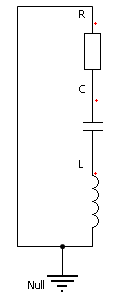
Wir beginnen mit dem Aufbau des Serienschwingkreises (Bild rechts) aus der durch einen Gyrator simulierten Spule (0,1...50 H), einem Drehkondensator (10..530 pF) und einem Serienwiderstand (50 Ω oder 1 kΩ). Laut Experimentieranleitung verwenden wir zuerst folgende Werte für die Bauelemente:

• C = 530 pF
• L = 10 H
• R = 1000 Ω

Wir beobachten mehrere Schwingungen (z.B. tStop=20 ms) ausgehend von einem auf 10 V aufgeladenen Kondensator:

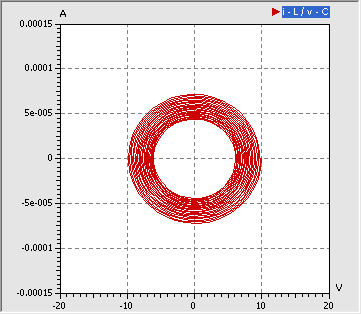
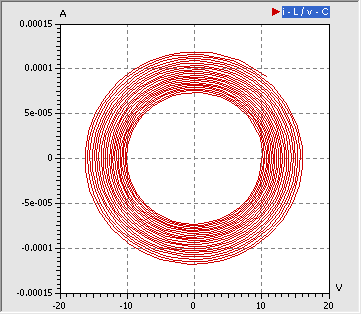
• Im Phasenraum widerspiegelt sich die durch den Serienwiderstand gedämpfte Schwingung als Spiral-Trajektorie in Richtung Koordinatenursprung [0,0]:
  
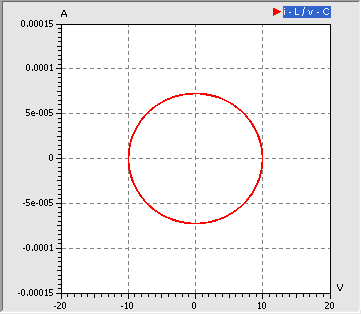
• Verringert man den Widerstand auf Null, so ergibt sich der Spezialfall der geschlossenen Trajektorie einer ungedämpften Schwingung:
  
• Realisiert man den Serienwiderstand durch eine aktive Schaltung, so lassen sich auch negative ohmsche Widerstände realisieren. So können wir mit R=-1000 Ω die letzte mögliche Form der Trajektorie im zweidimensionalen Phasenraum beobachten - die sich ins Unendliche entwickelnde Spirale:
  
• Für die weiteren Untersuchungen setzen wir den Serienwiderstand auf R=50 Ω. Damit ergibt sich eine nur leicht gedämpfte Schwingung.

Merke:
Die Trajektorie darf sich nicht kreuzen, ansonsten gäbe es ausgehend von einem Zustand mehr als eine weitere Entwicklungsmöglichkeit. Das ist in einem deterministischen System nicht möglich!

Fremderregter linearer Schwingkreis

Bevor wir einen Sinusgenerator an den Schwingkreis ankoppeln, um diesen in der Nähe seiner Resonanzfrequenz anzuregen, wollen wir die Schwingfrequenz unseres Kreises überprüfen:

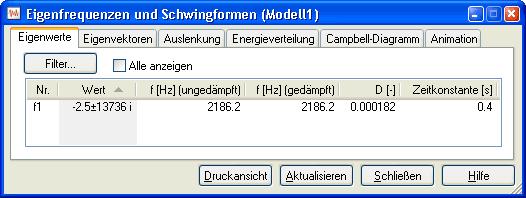
• Dazu muss man im SimulationX keine zusätzliche Signalverarbeitung in das Modell einbinden, wie wir dies zuvor zu Übungszwecken durchführten. SimulationX enthält ein Tool zur Analyse > Eigenfrequenzen und Schwingformen:
  
• Die angezeigte Frequenz von 2186,2 Hz steht im Widerspruch zu den ungefähr 1400 Hz, welche sich laut Experimentieranleitung bei dieser Konfiguration ergeben sollen!
• Wenn wir für die eingestellten Parameter die Resonanzfrequenz mit der Thomsonschen Schwingungsgleichung berechnen, werden sich 2186,16 Hz ergeben:

[math]\displaystyle{ f_0 = \frac{1}{2\pi\sqrt{LC}} }[/math]

Was ist hier schiefgelaufen?

• Die Genauigkeit eines Luftdrehkondensators wird durch die Toleranzen des geometrischen Aufbaus bestimmt. Damit dürfte die Kapazitätstoleranz im Bereich weniger Prozent liegen. Damit ist die große Abweichung der Resonanzfrequenz nicht erklärbar.
• Der Induktivitätswert wird mittels einer Gyratorschaltung aus einem Kapazitätswert gewonnen, wobei auch noch die aktuellen Werte von ohmschen Widerständen mit einfließen. Hier können größere Fehler entstehen!

Frage 9:
Wie groß ist die erforderliche Induktivität von L für den vorgegeben Wert C=530 pF, damit eine Resonanzfrequenz f₀=1400 Hz entsteht. Dieser Wert ist mittels der Analyse der Eigenfrequenzen zu überprüfen.

Den ermittelten Induktivitätswert behalten wir für die weiteren Experimente bei:

• Man kann davon ausgehen, dass im realen Experiment auch dieser Wert verwendet wurde, da sowohl die Frequenzmessung, als auch der Kapazitätswert des Drehkondensator nur mit geringen Toleranzen behaftet sind.
• Wahrscheinlich wurden am Zeiger der Gyrator-Induktivität 10 H gewählt und diesem Wert wurde ohne analytische Überprüfung vertraut!

Würden wir den Schwingkreis exakt mit der Resonanzfrequenz anregen, so gäbe es auf Grund der hohen Kreisgüte eine sehr große Resonanzüberhöhung:

• Den Kondensator versehen wir wieder mit der Anfangsspannung v0=0 V.
• Wir ergänzen eine sinusförmige Spannungsquelle aus der Modellbibliothek und benutzen eine Spannungsamplitude U_sin.V=1 V.
• Um das Umschlagen der Systemqualität anhand der Trajektorie im Phasenraum zu verdeutlichen, wählen wir eine Erregerfrequenz weit unterhalb der Resonanzfrequenz (U_sin.f=1000 Hz):

• Infolge der Fremderregung wird der Zustand des Gesamtsystems jetzt auch durch den aktuellen Wert der Betriebsspannung bestimmt. Es gibt also eine dritte Zustandsgröße, deren Koordinatenachse man sich im obigen Diagramm in der Tiefe vorstellen kann.
• Auch jetzt gibt es keine Kreuzungspunkte der Trajektorie. Wir sehen nur Kreuzungspunkte in der 2D-Projektion des Phasenraums, in Wirklichkeit verläuft die Trajektorie dort in unterschiedlichen Tiefen!
• Der zeitliche Verlauf der Kondensatorspannung ist nun nicht mehr sinusförmig, zeigt jedoch eine gewisse Periodizität:

• Diese Periodizität widerspiegelt sich auch in den Schleifen der Trajektorie im Phasenraum.

Fremderregter nichtlinearer Schwingkreis

Im nächsten Schritt ergänzen wir laut Anleitung die Diode D parallel zum Drehkondensator:

• Den Drehkondensator setzen wir auf seinen kleinsten Kapazitätswert C=10 pF.
• Die Diode erhält die von uns ermittelten Parameter cj0 und M, welche die Kapazitätskennlinie des Diodentyps BB 512 möglichst gut nachbilden.
• Wir verändern die Sinusspannung der Erregung vorläufig nicht (1 V bei 1000 Hz).
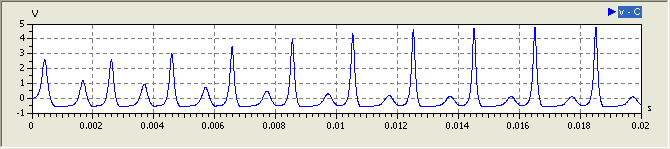
• Wie zu erwarten war, wird infolge des Gleichrichter-Effekts der Diode eine Halbwelle auf ca. 0,5 V begrenzt. Im Beispiel betrifft die die negative Halbwelle:

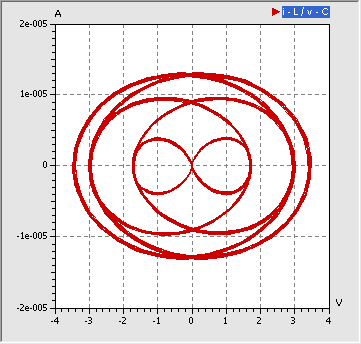
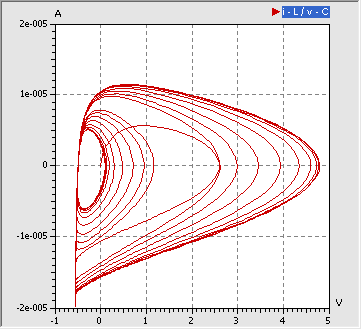
• Daraus resultiert eine qualitativ andere Trajektorie im Phasenraum:
  
• Wir werden später noch sehen, dass die Trajektorie in Abhängigkeit von der Frequenz und der Amplitude der Erregerspannung unterschiedliche Muster bildet. Diese Muster widerspiegeln die Amplitudencharakteristik des zeitlichen Verlaufs der Diodenspannung.

Frequenzspektrum des nichtlinearen Schwingkreises

Frequenzanalyse

Solange ein Schwingkreis ohne Fremderregung eine nur leichtgedämpfte Sinusschwingung ausführt, besteht das Frequenzspektrum nur aus seiner Resonanzfrequenz. Diese Frequenz konnten wir mittels Analyse > Eigenfrequenzen und Schwingformen ablesen. Dieses Tool ist jedoch sinnvoll nur für lineare Systeme nutzbar, da es sich um eine "Lineare Systemanalyse" handelt. Bei nichtlinearen Systemen könnte man nur die Schwingfrequenzen für den aktuellen Zustand sehen, für den das Modell linearisiert wird.

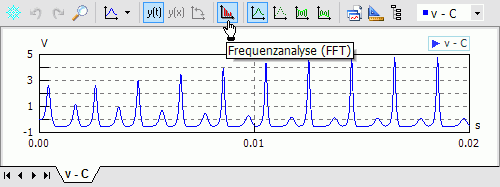
SimulationX bietet jedoch in den Signalfenstern die Analyse > Frequenzanalyse (FFT) :

• FFT ist die Abkürzung für Fast Fourier Transform (Schnelle Fourier-Transformation).
• Ein beliebiges zeitliches Signal lässt sich immer als Summe von Sinusschwingungen unterschiedlicher Frequenz und Amplitude hinreichend genau abbilden (Reihenentwicklung der Fourier-Analysis.

Die FFT setzt eine konstante Zeitschrittweite für das zu analysierende Signal voraus:

• Wir arbeiten bei der Aufzeichnung der Signale mit variablen Schrittweiten.
• Vor der FFT-Analyse erfolgt im SimulationX eine automatische Überführung in ein Signal mit konstanter Zeitschrittweite.
• Die Wahl dieser Schrittweite erfolgt automatisch auf Grundlage der kleinsten Aufzeichnungsschrittweite. Damit wird gleichzeitig der obere Grenzwert für das zu berechnende Spektrum festgelegt.
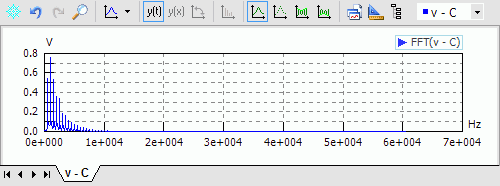
• Für den simulierten Spannungsverlauf an der Diode aktivieren wir die FFT-Analyse:
  
• Damit ergibt sich das folgende Frequenzspektrum in im ursprünglichen Ergebnis-Fenster:
  
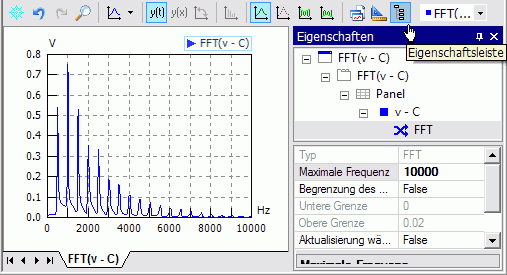
• Wird ein zu breites Spektrum berechnet, so begrenzen wir über die Eigenschaftsleiste diese Berechnung des Spektrums auf 10000 Hz, was der 10-fachen Erregerfrequenz entspricht:
  
• Man erkennt die Erregerfrequenz von 1000 Hz als Maximalanteil im Signal, gefolgt von der halben Frequenz.
• Alle Frequenzanteile sind Vielfache von 500 Hz. Der Anteil höherer Frequenzen im Spektrum sinkt stetig, das Spektrum endet praktisch bei ca. 9 kHz.
• Die Abtastschrittweite des Signalverlaufs muss hinreichend klein sein, um auch hohe Frequenzen noch erfassen zu können. Laut Abtasttheorem muss die Abtastfrequenz mindestens doppelt so hoch sein, wie die zu erfassende Frequenz. Das Abtasttheorem wird vom SimulationX bei der automatischen Ermittlung einer maximal möglichen Frequenz berücksichtigt.
• Für Spektrum-Anteile von 10 kHz benötigt man einen Signalwert mindestens aller 50 µs, was jedoch bereits zu sehr eckigen Signalverläufen führen würde.

Konfiguration der Anregung

Die Vielzahl von Frequenzanteilen resultiert aus dem Kappen einer Halbwelle, wenn die Durchlassspannung der "Gleichrichter"-Diode überschritten wird. Es entstehen "Knicke" im Spannungsverlauf, welche hohen Frequenzanteilen entsprechen.

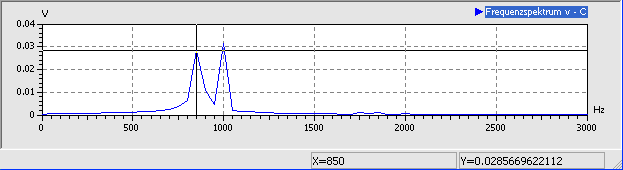
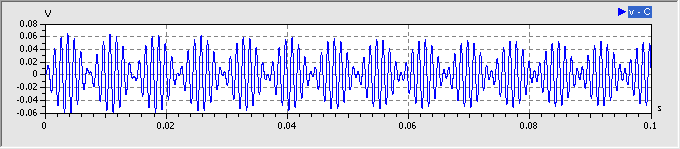
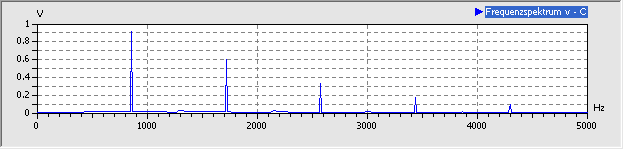
Wir verringern nun die Amplitude der Erregerspannung soweit, dass keine höherfrequenten Frequenzanteile mehr im Spektrum vorhanden sind. Das ist bei ca. 10 mV der Fall:

Zusätzlich zur Erregerfrequenz von 1 kHz erscheint die Resonanzfrequenz von ca. 850 Hz. Diese ergibt sich aus der Sperrschicht-Kapazität, die sich bei sehr kleinen Sperrspannungen einstellt und welche ungefähr Cj0 entspricht:

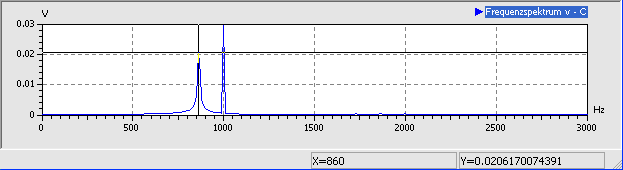
• Das Frequenzspektrum wird genauer berechnet, wenn man mehr Perioden der Schwingung simuliert. Mit tStop=0.1 s ergibt sich z.B. eine wesentlich feinere Auflösung, erkennbar an schmaleren Frequenz-Peaks. Die Resonanzfrequen wird jetzt im Beispiel mit 860 Hz ermittelt
  
• Der zugehörige Zeitverlauf der Diodenspannung zeigt die Schwebung von 140 Hz zwischen Erreger- und Resonanzfrequenz:
  

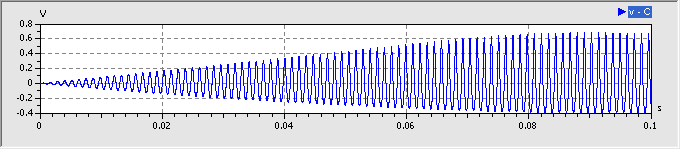
Wir erregen im Folgenden den Schwingkreis mit der zuletzt ermittelten Resonanzfrequenz von z.B. 860 Hz:

• Nun kommt es zu einem Aufschaukeln der Schwingung, bis infolge der vorhandenen Dämpfung in Reihenwiderstand und Diode ein Gleichgewicht erreicht ist (Resonanz-Überhöhung).
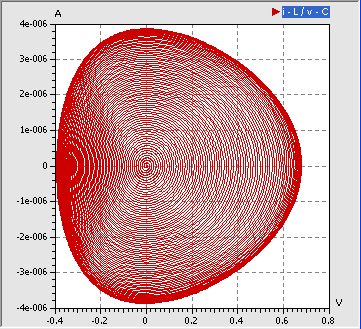
• Wir verringern die Erregungsamplitude soweit, dass innerhalb von 100 ms ein "sanfter" Übergang in den eingeschwungenen Zustand stattfindet:
  
• Die Konvergenz zu einem Endzustand gleicher Schwingungsamplitude widerspiegelt sich im 2D-Phasendiagramm in einer "Hervorhebung" der äußeren Trajektorienbahnen:
  
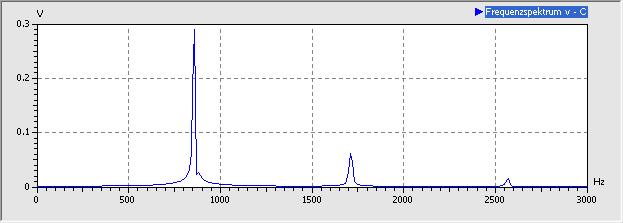
• Das Frequenzspektrum zeigt neben der Erregerfrequenz, welche nun der Resonanzfrequenz entspricht, kleine Amplituden der 1. und 2. Oberwelle:
  
• Die Oberwellen existieren, weil infolge der Amplitudenbegrenzung die Schwingung leicht von der Sinusform abweicht. Nur der reine Sinus besitzt keine Oberwellen.
• Wenn man sich die Grundfrequenz im Spektrogramm genauer anschaut, erkennt man einen kleinen Peak wenige Hz oberhalb der Erregerfrequenz. Durch die erhöhte Spannungsamplitude an der Diode verringerte sich deren Sperrschicht-Kapazität und damit verschob sich die Resonanzfrequenz etwas nach oben.

Einfluss der Anregungsamplitude

Wenn wir im Folgenden die Amplitude der Sinus-Erregung in kleinen Schritten vorsichtig erhöhen, so kommt der Gleichrichtungseffekt der Diode zur Wirkung. Das Kappen einer Halbwelle beginnt, wenn sich im Schwingkreis die Amplitude an der Diode auf über 0.5 V erhöht:

• Das Verhalten des Schwingkreises ändert sich qualitativ nicht bis zu einer bestimmten Erreger-Amplitude. Im Beispiel lag dieser Wert bei ungefähr 1 V. Bis dahin nimmt nur die Amplitude der Oberwellen im Spektrum kontinuierlich zu:
  
• Die Trajektorie konvergiert im 2D-Phasendiagramm weiterhin zu einer Trasse (Attraktor), weil sich die Amplitude der Schwingungen auf einen Endwert einschwingt. Das Einschwingen auf die Maximal-Amplitude erfolgt jetzt jedoch bedeutend schneller, als bei kleiner Erregungsamplitude:
  

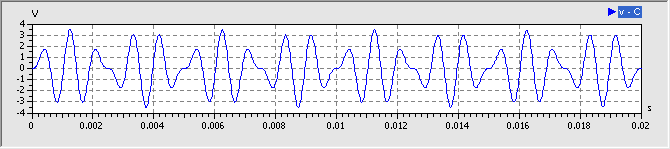
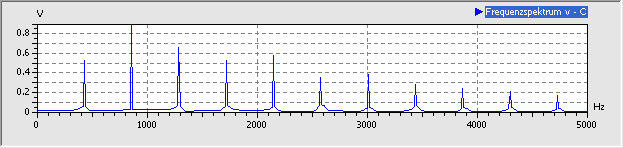
Eine neue Qualität des Verhaltens entsteht, indem bei einer weiteren Erhöhung der Erregungsamplitude plötzlich eine Perioden-Verdopplung stattfindet. Im Beispiel war dies bei 1.3 V Erregungsamplitude der Fall. Es tritt dann die 1. Subharmonische der Erregungsfrequenz im Frequenzspektrum auf:

• Von dieser 1. Subharmonischen leiten sich zusätzliche Obertöne im Frequenzspektrum ab. Das Spektrum erstreckt sich bis über 10 kHz (im Bild beschnitten).
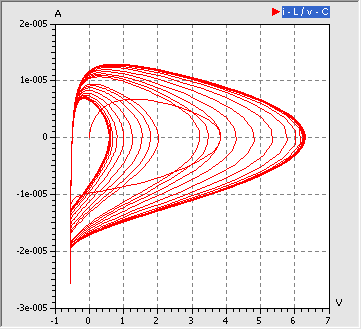
• Im 2D-Phasendiagramm bildet sich der Atraktor jetzt in Form zweier Trassen ab:
  
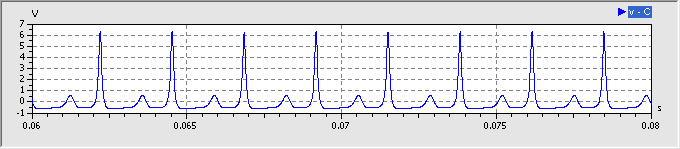
• Ursache für die 2 Attraktor-Trassen ist die unterschiedliche Schwingungsamplitude der beiden Perioden nach der Periodenverdopplung. Dies zeigt ein Ausschnitt aus dem zeitlichen Schwingungsverlauf deutlich:
  

Bifurkation

Nichtlineare Systeme, deren Verhalten von einem Parameter (hier der Anregungsamplitude) abhängt, können bei einer Änderung des Parameters ihr Verhalten plötzlich ändern. Wie im Beispiel kann ein System, das zuvor einem Grenzwert zustrebte, nun zwischen zwei Werten hin und her springen, also zwei Häufungspunkte aufweisen. Dies nennt man eine Bifurkation.

Bifurkationsdiagramm

Solche Verzweigungen des Systemverhaltens (Bifurkationen) lassen sich in Bifurkationsdiagrammen graphisch darstellen, was insbesondere bei der Abhängigkeit von nur einem Parameter sehr anschaulich ist:

• Die X-Achse wird mit dem veränderliche Parameter belegt. Das sollte bei uns die Amplitude der anregenden Sinus-Spannung sein.
• Die Y-Achse sollte eine markante Systemgröße darstellen, welche die angestrebten Grenzwerte repräsentiert. In unserem Beispiel ist das die Amplitude der Diodenspannung, welche nach der Verzweigung zwischen den beiden Wert schwankt.
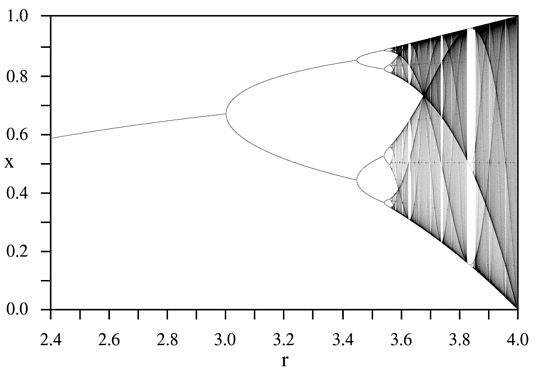
• Ein markantes Beispiel ist das Bifurkationsdiagramm der logistischen Gleichung (Bildquelle: Wikimedia Commons):

Wir werden unser Modell so erweitern, dass wir den Verhaltensumschlag infolge der Verdopplung der Periodendauer in solch einem Bifurkationsdiagramm darstellen können. Dafür sind größere Umbauten im Modell erforderlich. Deshalb erzeugen wir eine Kopie unserer bisherigen Modelldatei und arbeiten mit dieser Kopie weiter:

Hinweis: Die Parallelkapazität zur Diode von 10 pF musste entfernt werden, weil es ansonsten zu numerischen Problemen mit dem ereignisgesteuerten Abtastglied kommt. Das Verhalten ändert sich dadurch praktisch nicht!

Leider kann man das bisherige Modell-Element der sinusförmigen Spannungsquelle nur mit einer konstanten Amplitude betreiben. Wir wollen im Simulationszeitbereich die Amplitude jedoch in einem vorgegebenem Bereich variieren:

• Wir müssen deshalb eine Spannungsquelle mit Signaleingang verwenden.
• Diese speisen wir mit dem Ausgang eines Signalgenerators, dessen Amplitude wir über seinen Eingang x steuern.
• Die Steuerung für einen vorläufigen Amplitudenbereich der Sinus-Amplitude von 0,9...1,3 V übernimmt ein Function-Block mit

0.9+0.4*(t-tStart)/(tStop-tStart)

• Damit der Schwingkreis genügend Zeit hat, der Spannungsänderung zu folgen, erhöhen wir die Simulationszeit auf tStop=0,5 s. Damit ergibt sich ein Verlauf der Diodenspannung, welcher deutlich die Aufspaltung in zwei Amplitudengrenzwerte zeigt:

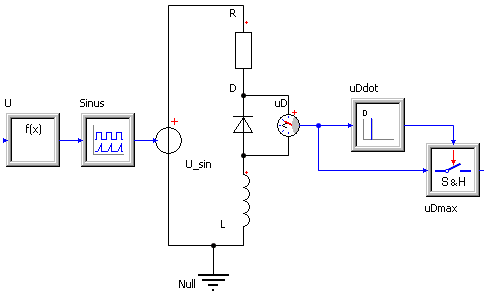
Das Ergänzen der uDmax-Erfassung sollte mit unseren bisherigen Erfahrungen auch kein Problem sein:

• Mit einem Differenzierer bilden wir die zeitliche Ableitung uDdot.y der gemessenen Kondensatorspannung.
• Die Nulldurchgänge von uDdot.y "von oben nach unten" kennzeichnen die Maxima der Kondensatorspannung uD.v. An diesen Stellen wird der Wert der Kondensatorspannung als uDmax.y übernommen.
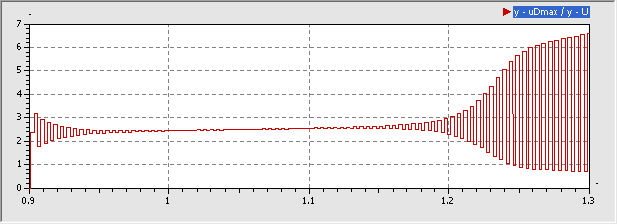
• Die Darstellung uDmax.y=f(U.y) ergibt das gewünschte Bifurkationsdiagramm:

• Am Anfang erkennt man den Einschwingvorgang infolge des Einschaltens der Sinusspannung von 0,9 V. Für den eingeschwungenen Betrieb bei 0,9 V ist jedoch der eine Grenzwert typisch.
• Erst nach dem Überschreiten von 1,2 V kommt es zum Aufspalten in zwei Grenzwerte.

Der Weg zum perfekten Chaos

Mit etwas Geduld und Experimentierfreude gelangt man sicher durch systematisches Probieren irgendwann zum perfekten Chaos. Um im Rahmen der knapp bemessenen Übungszeit die gewünschten Effekte beobachten zu können, sollen hier einige Erkenntnisse des Autors einfließen:

• Beim Durchfahren der Anregungsamplitude von nahe Null bis zu einem Maximalwert müssen hinreichend viele Periodenverdopplungen stattfinden, damit Chaos entsteht. In der Experiment-Anleitung wurde von 4 Periodenverdopplungen gesprochen. Leider wird dies mit der eingestellten Erregerfrequenz wahrscheinlich nicht gelingen.
• Es ist günstig, im bisher betrachteten Bereich möglichst schnell zu Periodenverdopplungen zu kommen. Das gelingt, indem man die Anregungsfrequenz etwas erhöht. Im Beispiel war das bei einer Erhöhung um ca. 20% von 860 Hz auf 1000 Hz der Fall.
• Man durchfährt eine Anregungsamplitude von 0...15 V in einer Simulationszeit von 2 s.
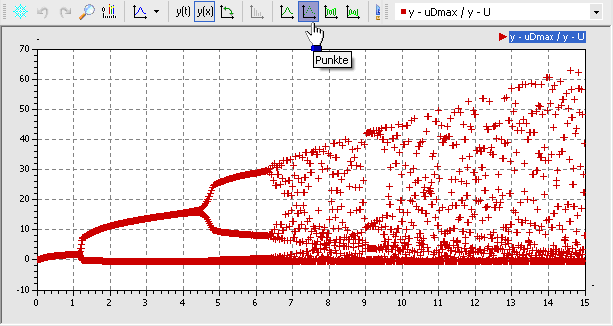
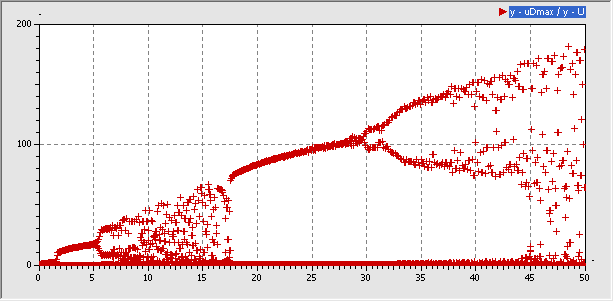
• Da die jeweiligen Perioden-Maxima im Ergebnisfenster standardmäßig mit Linien verbunden werden, kann man die Bifurkationen nur schlecht erkennen. Wenn man anstatt der Liniendarstellung die Darstellung der Punkte aktiviert, so erhält man ein klassisches Bifurkationsdiagramm:
  
• In der Hoffnung, dass die Sperrschicht der Diode nicht durchschlägt, kann man die Anregungsamplitude z.B. bis auf 50 V ansteigen lassen. Man erkennt dann im Bereich von 20...30 V ein Gebiet relativer Ordnung, bevor oberhalb davon wieder das Chaos beginnt:
  

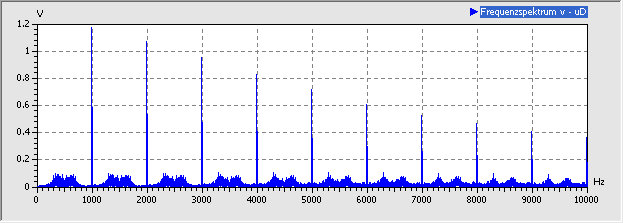
Um das Verhalten z.B. bei 15 V Anregungsamplitude zu untersuchen, verwendet man im Generator einen konstanten Amplitudenwert von 15 V (anstatt self.x):

• Unterhalb der Anregungsfrequenz und zwischen ihren Harmonischen ist nun im Spektrum Rauschen sichtbar, d.h. alle Frequenzen sind vertreten.
• Das obige Spektrum kann man als Beginn des chaotischen Verhaltens interpretieren.
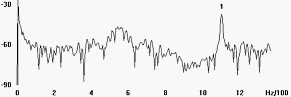
• "Perfektes Chaos" wäre durch ein intensives Rosa Rauschen gekennzeichnet. Leider kann man das wahrscheinlich mit unserem Simulationsmodell nicht so einfach oder gar nicht erreichen.
• Im realen Experiment (Siehe PDF-Datei) ist es jedoch durch feinfühlige Abstimmung möglich, solch einen Zustand zu erreichen. Dies zeigt ein Bild mit dem Frequenzbereich unterhalb der dort verwendeten Erregerfrequenz von ca. 1100 Hz:
  

Der Weg war das Ziel - auch der zum perfekten Chaos!

← →