Software: CAD - Tutorial - Optimierung: Unterschied zwischen den Versionen

Aus OptiYummy
Zur Navigation springenZur Suche springen
KKeine Bearbeitungszusammenfassung
KKeine Bearbeitungszusammenfassung
 
(51 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
[[Software:_CAD_-_Tutorial|&uarr;]] <div align="center"> [[Software:_CAD_-_Tutorial|&larr;]] [[Software:_CAD_-_Tutorial_-_Optimierung_-_OptiY|&rarr;]] </div>
[[Software:_CAD_-_Tutorial|&uarr;]] <div align="center"> [[Software:_CAD_-_Tutorial|&larr;]] [[Software:_CAD_-_Tutorial_-_Optimierung_-_OptiY|&rarr;]] </div>
<div align="center">'''7. Übung im CAD-Tutorial'''</div>
<div align="center">'''5. Übung im CAD-Tutorial'''</div>
<div align="center"> ''' Nennwert- und Toleranzoptimierung (Biegefeder) ''' </div>
<div align="center"> ''' Nennwert- und Toleranzoptimierung (Biegefeder) ''' </div>
<div align="center">[http://www.ifte.de/mitarbeiter/kamusella.html '''Autor: Dr.-Ing. Alfred Kamusella''']</div>
<div align="center">[https://www.ifte.de/mitarbeiter/kamusella.html '''Autor: Dr.-Ing. Alfred Kamusella''']</div>
<div align="center">'''''-- Dieses Script wird zur Zeit erarbeitet! --'''''</div>


<div align="center"> '' Pessimisten sind Optimisten mit mehr Erfahrung. '' </div>
<div align="center"> '' Pessimisten sind Optimisten mit mehr Erfahrung. '' </div>
<div align="center"> '' - Deutsches Sprichwort - '' </div>
<div align="center"> '' - Deutsches Sprichwort - '' </div>
'''''Hinweis:''' <br>Zur Einarbeitung in die Simulation von Maß-Toleranzketten wird vorbereitend die individuelle Bearbeitung des Beispiels [[Software:_OptiY-Workflow_-_Einfache_Toleranzkette|'''"Einfache Toleranzkette"''']] empfohlen.''


Die grundlegenden physikalisch-konstruktiven Zusammenhänge zu Biegefedern und der Bestimmung ihrer Resonanzfrequenz findet man im Wikipedia-Artikel [http://de.wikipedia.org/wiki/Durchschlagende_Zunge#Berechnung_der_Tonh.C3.B6he '''"Durchschlagende Zunge"''']. 
'''Biegefeder-Aufgabe:''' Mit einem vorgegebenem Material ist eine optimale Biegefeder mit der Federkonstante '''C<sub>soll</sub>''' zu dimensionieren, welche bestimmte Forderungen trotz der unvermeidbaren Fertigungstoleranzen erfüllt:


Mit einem vorgegebenem Material ist eine optimale Biegefeder mit der Federkonstante '''C<sub>soll</sub>''' zu dimensionieren, welche bestimmte Forderungen trotz der unvermeidbaren Fertigungstoleranzen erfüllt:
'''Abmessungen''' der einseitig eingespannte Biegefeder mit rechteckigem Querschnitt:[[Datei:Software_CAD_-_Tutorial_-_Optimierung_-_Biegefeder.gif|right|.]]
* '''Abmessungen''' der einseitig eingespannte Biegefeder mit rechteckigem Querschnitt:
* '''L''' = Länge
*# '''L''' = Länge
* '''b''' = Breite des Querschnitts
*# '''b''' = Breite des Querschnitts
* '''t''' = Dicke (Thickness) des Querschnitts mit '''t&nbsp;≤&nbsp;b'''
*# '''t''' = Dicke (Thickness) des Querschnitts mit '''t&nbsp;<&nbsp;b'''
 
* '''Anforderungen''':
'''Anforderungen''':
*# '''C<sub>soll</sub>''' = '''(140+xx)&nbsp;N''' (zu realisierende Federkonstante mit Teilnehmernummer '''xx'''=01..99)  
* '''C<sub>soll</sub>''' = '''(140+xx)&nbsp;N/m''' (Federkonstante für Teilnehmer-Nr. '''xx'''=01..99)  
*# '''C<sub>Tol</sub>''' = '''0,2''' (zulässige Toleranzbreite der Federkonstante in 100%)
* '''C<sub>Tol</sub>''' = '''0,2''' (zulässige Toleranzbreite der Federkonstante in 100%) = '''±10%'''
*# '''F<sub>Max</sub>''' = '''1&nbsp;N''' (maximal auftretende Kraft)
*  '''ΔT''' &nbsp;= '''20&nbsp;°C&nbsp;±50&nbsp;K''' (Bereich der Umgebungstemperatur)
*# '''f<sub>Resonanz</sub>''' = '''möglichst groß''' (Resonanzfrequenz der Grundschwingung)
* '''F<sub>Max</sub>''' = '''1&nbsp;N''' (max. auftretende Kraft)
*# '''E<sub>Modul</sub>''' = entsprechend des gewählten Materials ("'''Stahl, geschmiedet'''" aus Bibliothek)
* '''f<sub>Resonanz</sub>''' = '''möglichst groß''' (Frequenz der Grundschwingung)
*# '''<big>σ</big><small>b<sub>zul</sub></small>''' = Biegefließgrenze entsprechend des gewählten Materials
* '''E<sub>Modul</sub>''' = entsprechend des gewählten Materials ("'''Stahl, geschmiedet'''" aus Bibliothek)
* '''<big>σ</big><small>b<sub>zul</sub></small>''' = Biegefließgrenze entsprechend des gewählten Materials


'''A. Nennwert-Optimierung:'''
'''A. Nennwert-Optimierung:'''
Zeile 32: Zeile 33:
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Zusammenfassung|Zusammenfassung]]
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Zusammenfassung|Zusammenfassung]]
'''B. Toleranz-Analyse:'''
'''B. Toleranz-Analyse:'''
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Probabilistische_Simulation|Probabilistische Simulation]]
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Toleranzen_im_CAD-Modell|Toleranzberechnungen im CAD-Modell]]
# ...
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Feder-Toleranzen|Toleranzen der Biegefeder]]
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Probabilistik|Probabilistische Simulation]]
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Probabilistik_Experiment|Experiment-Konfiguration]]
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Probabilistik_Sampling-Methode|Statistische Versuchsplanung - Sampling Methode]]
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Probabilistik_Visualisierung|Visualisierung und Interpretation]]
'''C. Toleranz-Optimierung:'''
'''C. Toleranz-Optimierung:'''
# ...
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Toleranzen_-_Robust-Design|Robust-Design-Optimierung (Einführung)]]
# ...
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Toleranzen_-_Experimentkonfiguration|Experimentkonfiguration]]
# [[Software:_CAD_-_Tutorial_-_Optimierung_-_Toleranzen_-_Ergebnisse|Ergebnisse]]
'''Einzusendende Ergebnisse:'''<br>   
'''Einzusendende Ergebnisse:'''<br>   
* Teilnehmer der Lehrveranstaltung [http://www.ifte.de/lehre/cad/index.html '''"CAD-Konstruktion"'''] schicken die Ergebnisse an '''a.kamusella[[Bild:Char-ed.gif]]ifte.de''' .
* Teilnehmer der Lehrveranstaltung [https://www.ifte.de/lehre/cad/index.html '''"CAD-Konstruktion"'''] laden die Ergebnisse im [https://bildungsportal.sachsen.de/opal/auth/RepositoryEntry/31733940224/CourseNode/1629858745120506011 Opalkurs] hoch.
* Als Anhang dieser Mail mit (xx=Teilnehmer-Nummer 01...99) ist das gesamte CAD-Projekt einschließlich der .OPY-Datei in einem Archiv-File (z.B. '''Feder_xx.ZIP''') zu senden.
* Als Lösung (xx=Teilnehmer-Nummer 01...99) sind die vollständig konfigurierten Dateien '''Feder_xx.ipt''' und '''Feder_xx.OPY''' sowie der ausgefüllte Antwortbogen ('''CAD-Antwort_5_xx.pdf''') in einem Archiv-File ('''Feder_xx.ZIP''') zu senden:
* Einsendeschluss ist die Nacht vor dem Termin des nächsten Übungskomplexes. Die Nacht endet morgens um 10:00 Uhr.<div align="center"> [[Software:_CAD_-_Tutorial|&larr;]] [[Software:_CAD_-_Tutorial_-_Optimierung_-_OptiY|&rarr;]] </div>
** In den Experimenten müssen aussagekräftige Diagramme zur Visualisierung der jeweiligen Experiment-Prozesse und -Ergebnisse konfiguriert sein.  
** Die Bauteil-Datei muss die ermittelten optimalen Maße und zugehörigen Toleranzen enthalten.
** Im bereitgestellten Antwortbogen sind die optimalen Nennwerte und die damit ermittelten Bewertungsgrößen aufzulisten. 
* Einsendeschluss ist die Nacht vor dem Termin des nächsten Übungskomplexes. Die Nacht endet morgens um 10:00 Uhr.
<div align="center"> [[Software:_CAD_-_Tutorial|&larr;]] [[Software:_CAD_-_Tutorial_-_Optimierung_-_OptiY|&rarr;]] </div>

Aktuelle Version vom 25. August 2021, 08:12 Uhr

↑

5. Übung im CAD-Tutorial
Nennwert- und Toleranzoptimierung (Biegefeder)
Pessimisten sind Optimisten mit mehr Erfahrung.
- Deutsches Sprichwort -

Hinweis:
Zur Einarbeitung in die Simulation von Maß-Toleranzketten wird vorbereitend die individuelle Bearbeitung des Beispiels "Einfache Toleranzkette" empfohlen.

Biegefeder-Aufgabe: Mit einem vorgegebenem Material ist eine optimale Biegefeder mit der Federkonstante Csoll zu dimensionieren, welche bestimmte Forderungen trotz der unvermeidbaren Fertigungstoleranzen erfüllt:

Abmessungen der einseitig eingespannte Biegefeder mit rechteckigem Querschnitt:

.
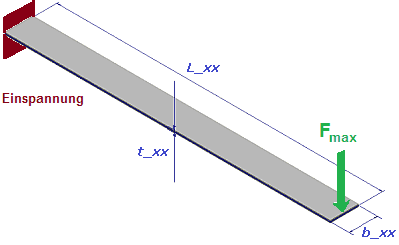
  • L = Länge
  • b = Breite des Querschnitts
  • t = Dicke (Thickness) des Querschnitts mit t ≤ b

Anforderungen:

  • Csoll = (140+xx) N/m (Federkonstante für Teilnehmer-Nr. xx=01..99)
  • CTol = 0,2 (zulässige Toleranzbreite der Federkonstante in 100%) = ±10%
  • ΔT  = 20 °C ±50 K (Bereich der Umgebungstemperatur)
  • FMax = 1 N (max. auftretende Kraft)
  • fResonanz = möglichst groß (Frequenz der Grundschwingung)
  • EModul = entsprechend des gewählten Materials ("Stahl, geschmiedet" aus Bibliothek)
  • σbzul = Biegefließgrenze entsprechend des gewählten Materials

A. Nennwert-Optimierung:

  1. Optimierungs- und Analysetool (OptiY)
  2. Parametrisiertes CAD-Modell
  3. Physikalische und konstruktive Zusammenhänge (Regeln)
  4. Optimierungsworkflow
  5. Globale Suche
  6. Lokale Suche
  7. Zusammenfassung

B. Toleranz-Analyse:

  1. Toleranzberechnungen im CAD-Modell
  2. Toleranzen der Biegefeder
  3. Probabilistische Simulation
  4. Experiment-Konfiguration
  5. Statistische Versuchsplanung - Sampling Methode
  6. Visualisierung und Interpretation

C. Toleranz-Optimierung:

  1. Robust-Design-Optimierung (Einführung)
  2. Experimentkonfiguration
  3. Ergebnisse

Einzusendende Ergebnisse:

  • Teilnehmer der Lehrveranstaltung "CAD-Konstruktion" laden die Ergebnisse im Opalkurs hoch.
  • Als Lösung (xx=Teilnehmer-Nummer 01...99) sind die vollständig konfigurierten Dateien Feder_xx.ipt und Feder_xx.OPY sowie der ausgefüllte Antwortbogen (CAD-Antwort_5_xx.pdf) in einem Archiv-File (Feder_xx.ZIP) zu senden:
    • In den Experimenten müssen aussagekräftige Diagramme zur Visualisierung der jeweiligen Experiment-Prozesse und -Ergebnisse konfiguriert sein.
    • Die Bauteil-Datei muss die ermittelten optimalen Maße und zugehörigen Toleranzen enthalten.
    • Im bereitgestellten Antwortbogen sind die optimalen Nennwerte und die damit ermittelten Bewertungsgrößen aufzulisten.
  • Einsendeschluss ist die Nacht vor dem Termin des nächsten Übungskomplexes. Die Nacht endet morgens um 10:00 Uhr.
Abgerufen von „http:///index.php?title=Software:_CAD_-_Tutorial_-_Optimierung&oldid=25327“