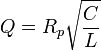Software: SimX - Einfuehrung - Elektro-Chaos - Schwingkreis

↑

← →

Elektrischer Schwingkreis

Ein elektrischer Schwingkreis ist eine resonanzfähige elektrische Schaltung aus einer Spule (L) und einem Kondensator (C), die elektrische Schwingungen ausführen kann. In realen Schwingkreisen muss man immer eine ohmsche Verlustleistung berücksichtigen, welche überwiegend aus dem ohmschen Widerstand (R) des Spulendrahtes resultiert.

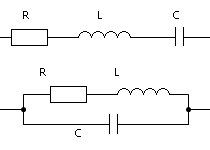
Je nach Anordnung der Induktivitäten und Kapazitäten unterscheidet man zwischen Reihenschwingkreis und Parallelschwingkreis. Wir untersuchen zuerst die Resonanz eines Reihenschwingkreises, um danach mit den gesammelten Erfahrungen die analogen Experimente an einem Parallelschwingkreis durchzuführen.

Die Resonanzfrequenz eines idealen verlustfreien (R=0) Schwingkreises mit konstanten Werten für L und C berechnet sich zu

[math]\displaystyle{ f_0 = \frac{1}{2 \pi \sqrt{L C}} }[/math]

Da zumindest die Spule in realen Schwingkreisen immer einen ohmschen Widerstand R des Drahtes aufweist (Ausnahme: Supraleitfähigkeit), ist die reale Resonanzfrequenz f_r etwas geringer, als die nach obiger Thomsonschen Schwingungsgleichung berechnete Frequenz f₀:

[math]\displaystyle{ f_{\mathrm r} = \frac{1}{2\pi}\sqrt{\frac{1}{LC} -\frac{{R_L}^2}{L^2}} }[/math]

Reihenschwingkreis

Wir werden im SimulationX das Modell eines Serienschwingkreis aufbauen, welcher mit einer Frequenz f₀=1 kHz schwingt (Modell-Datei: Reihenschwingkreis.ism). Dazu steht uns eine Luftspule mit einer Induktivität L= 1mH zur Verfügung. Die Spule besitzt einen Drahtwiderstand R=1,3 Ω. Den erforderlichen Kondensator berechnen wir mit der Thomsonschen Schwingungsgleichung.

• Wir beachten, dass eine elektronische Schaltung auch als Modell ein Nullpotential benötigt:
  
• In obiger Schaltung kann es noch nicht zu Schwingungen kommen, weil eine Anregung fehlt und der Kreis noch nicht geschlossen ist. Um später beliebige Anregungen generieren zu können, benutzen wir eine Spannungsquelle U mit Signaleingang:
  
• Beachte: Der Innenwiderstand dieser idealisierten Spannungsquellen ist gleich Null. Praktisch bedeutet dies, dass sich die Quelle bei u=0 wie ein durchgehender Leiter verhält.
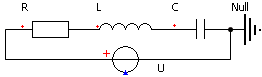
• Diese Schaltung kann man ohne äußere Anregung zum Schwingen bringen, wenn man einen aufgeladenen Kondensator einbaut:

1. Wir setzen die Anfangsspannung C.v0=10 V.
2. Da durch alle in Reihe geschalteten Bauelemente der gleiche Strom fließt, können wir das Stromsignal eines beliebigen Bauelements (außer des Null-Leiters) betrachten.
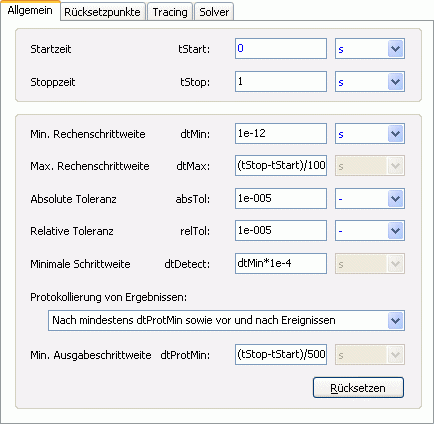
3. Wir simulieren einen Zeitbereich von 10 ms und konfigurieren die Rechen- und Protokollschrittweiten so, dass saubere Sinusschwingungen abgebildet werden:
   

• Wenn eine komplette Sinusperiode T=1 ms erfordert, so haben wir damit den zuvor berechneten Wert für die elektrische Kapazität bestätigt. Die Frequenz beträgt dann f=1/T=1 kHz.
• Anderenfalls haben wir uns verrechnet und müssen den geforderten Kondensatorwert noch richtig ermitteln.

Frage 3: Was ist der erforderliche Wert für die Kapazität C?

Wir werden im Folgenden den Schwingkreis mit einer variablen Sinusfrequenz anregen, um die Erhöhung der Schwingungsamplitude im Resonanzfall zu beobachten:

• Wir nutzen nun wieder einen am Anfang entladenen Kondensator (C.v0=0 V).
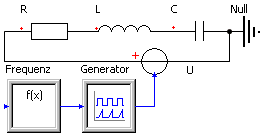
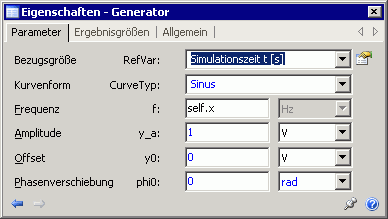
• Wir ergänzen das Modell um einen Signalgenerator (Signalglieder→Quellen), dessen Frequenz wir über seinen Signaleingang self.x vorgeben:
  
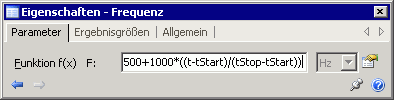
• Mittels eines f(x)-Signalgliedes programmieren wir im simulierten Zeitbereich eine lineae Erhöhung der Generator-Frequenz ausgehend von einer unteren Frequenz f_u=500 Hz um den Frequenzbereich f_B=1000 Hz:
  
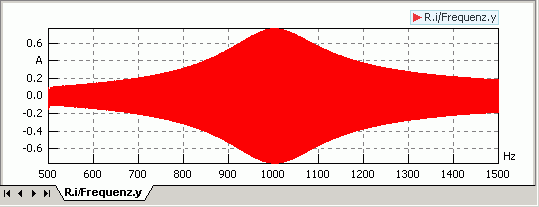
• Es genügt eine Simulationszeit von tStop=1 s, um den gesamten Frequenzbereich hinreichend langsam zu scannen. Die y(x)-Darstellung des Stromes i über die Anregungsfrequenz sollte das folgende Verhalten ergeben:
  
• y(x)-Darstellung: Beide Signale in ein gemeinsames Ergebnisfenster-Panel ziehen und von y(t)- auf y(x)-Darstellung umschalten. Die Zuordnung zu den Achsen kann nachträglich vertauscht werden.
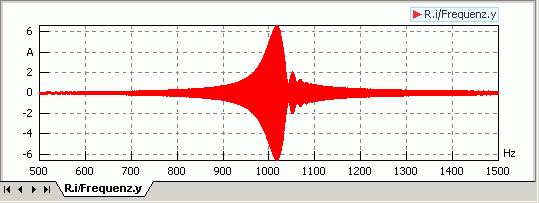
• Die Resonanzüberhöhung dieses Schwingkreises ist zwar deutlich, aber nicht sehr groß. Ursache ist die Dämpfung infolge des Spulenwiderstands von R=1,3 Ω. Verwendet man eine Spule mit einem Zehntel dieses Wertes R=0,13 Ω, so fällt Resonanzüberhöhung wesentlich markanter aus:
  
• Hinweise: Die Einbrüche in der Hüllkurve nach Überschreiten der Resonanzfrequenz resultieren aus der relativ schnellen Änderung der Anregungsfrequenz. Vergrößert man die Simulationszeit auf z.B. 5 s, so verschwindet dieser Effekt. Auch wird die Lage des Resonanz-Maximum etwas genauer berechnet. Leider vergrößert sich dadurch wesentlich die Berechnungszeit. Da uns die Einbrüche in der Hüllkurve für die weitere Bearbeitung nicht stören, können wir den Wert tStop=1 s behalten.

Reihenschwingkreis - Signalverarbeitung

Frage 4: Welche Kreisgüte Q ergibt sich bei einen Drahtwiderstand von R=1,3 Ω?
Der aus der Simulation durch Ausmessen der Grenzfrequenzen (Bandbreite B) zu ermittelnde Güte-Wert des Serienschwingkreises:

ist mit dem analytisch bestimmten Wert zu vergleichen:

[math]\displaystyle{ Q = \frac1R \sqrt{\frac LC} }[/math]

f₀ setzt sich aus dem geometrischen Mittel

der oberen f₂ und der unteren Grenzfrequenz f₁ zusammen. Die Grenzfrequenzen f₁ bzw. f₂ sind diejenigen Frequenzen, bei denen die Spannung U bzw. der Strom I auf den 1/√2≈0,707-fachen Wert des Maximalwertes zurückgehen. An dieser Stelle ist die Leistung im Schwingkreis nur noch halb so groß wie bei der Resonanzfrequenz.

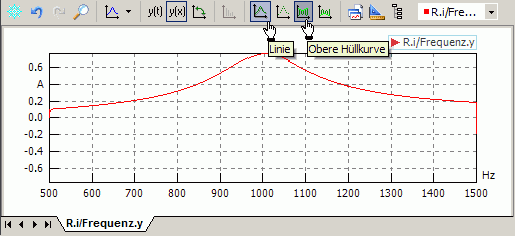
Das direkte Ausmessen der Amplituden der dargestellten sinusförmigen Signalverläufe mit dem Cursor ist kaum praktikabel. Sinnvoll wäre hierfür die Verwendung z.B. der oberen Hüllkurve:

• In den Ergebnisfenstern kann z.B. die obere Hüllkurve eingeblendet werden. Damit man die Hüllkurve erkennt, muss man die Linien der Originalkurve ausblenden:
  
• Leider finktioniet das Messen mit eingeblendeter Hüllkurve nicht besser als ohne. Der Messcursor folgt weiterhin dem unsichtbaren Originalsignal (oszilliert in vertikaler Richtung).
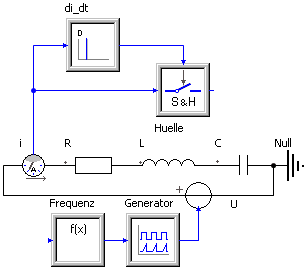
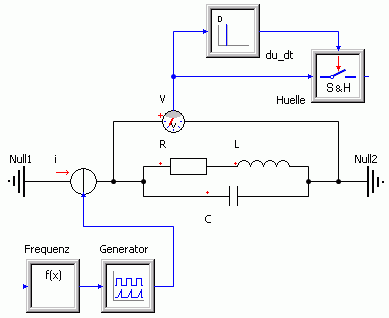
• Wir ergänzen deshalb unseren Simulationsversuchsstand um eine Signalverarbeitung, welche die Hüllkurve der Strom-Maxima direkt als Modellgröße liefert. Die erforderlichen Bausteine für die Signalverarbeitung stehen in der Modellbibliothek zur Verfügung:
  

1. Ein analoger Stromsensor liefert uns die aktuellen Stromwerte.
2. Das spezielle Signalglied "Ereignisgesteuertes Abtastglied" (Sample&Hold) soll möglichst exakt die Maximalwerte der einzelnen Sinusschwingungen erfassen (Sample) und bis zum nächsten Maximalwert den Wert als Ausgangssignal bereitstellen (Hold).
3. Die Zeitpunkte der Sample-Triggerimpulse werden durch die Nulldurchgänge der zeitlichen Stromableitung bestimmt (Siehe: Kurvendiskussion). Dazu verwenden wir das lineare Signalglied Differenzierer (D-Glied) mit Verstärkung G=1 und Vorhaltezeit Td=1 s:

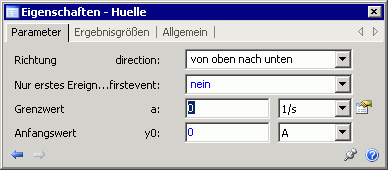
Entscheidend für die richtige Erfassung der Hüllkurve ist die korrekte Konfiguration des ereignisgesteuerten Abtastgliedes:

• Das Erfassen des aktuellen Stromwertes soll bei di/dt=0 A/s erfolgen. Die "Auslösung" des Triggerimpulses wird über den Grenzwert a=0 A/s für das Steuersignal definiert. (Hinweis: In Ermangelung der Einheit A/s im SimulatinX wurde der Gradient 1/s als Ersatz verwendet!)
• Wir wollen nur die obere Hüllkurve erfassen. Diese wird durch die Maxima des Stromsignals gebildet. Die 2. Ableitung des Stromes ist in den Maxima negativ, was durch direction=von oben nach unten definiert wird.
• Da alle Maxima des Stromsignals zu erfassen sind, muss firstevent=nein gwählt werden.

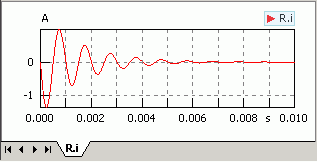
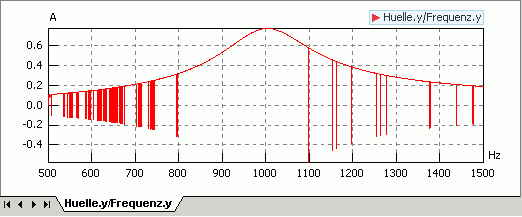
Im Ergebnis der Simulation sollte mit tStop=1 s, dtMin=1e-12 s und "exakter" Darstellung der Ereignispunkte ungefähr folgende Hüllkurve berechnet werden:

• Es werden einzelne Punkte erfasst, welche zur unteren Hüllkurve (den Minima) gehören.
• Die Simulation im Zeitbereich erfolgt mit einer sich automatisch anpassenden Zeitschrittweite dt. Diese Schrittweite wird so geregelt, dass die Berechnung mit einer hinreichenden Genauigkeit erfolgt.
• Zusätzlich versucht der Solver mit der sogenannten Ereignisbehandlung, markante Zeitpunkte möglichst exakt anzusteuern. Zu diesen "markanten" Zeitpunkten gehören die Auslösezeitpunkte für die Sample-Triggerimpulse.
• Hierbei erfolgen augenscheinlich Fehlauslösungen, weil die Simulationssteuerung noch nicht richtig konfiguriert ist. Im Beispiel wurden folgende Werte für die allgemeinen Einstellungen verwendet:
  
• Für numerisch unkritische Simulationen genügt meist die Einstellung des gewünschten Zeitbereiches und eine Anpassung der Schrittweitenparameter, um optisch "schöne" Signalverläufe zu erhalten.
• Treten jedoch unvorhergesehene Schwierigkeiten auf, wie wir sie bei der Hüllkurvenerfassung beobachten, ist ein gewisses Erfahrungswissen erforderlich. Das ist ähnlich wie beim Autofahren: je kritischer die Straßenverhältnisse sind, desto feinfühliger muss man lenken, Gas geben und bremsen.

Für unser Beispiel wird hier eine Lösung vorgeschlagen, die hoffentlich bei allen funktioniert:

• Im Normalfall stört ein sehr kleiner Wert für dtMin nicht, da eine automatische Schrittweitenregelung für dt erfolgt.
• Das ändert sich jedoch, wenn eine Ereignisbehandlung stattfinden muss. Nachdem ein Ereigniszeitpunkt möglichst exakt angesteuert wurde, beginnt die Simulation nach dem Ereignis wieder mit der Schrittweite dt=dtMin.
• Wie wir sehen, kann es durch numerische Ungenauigkeiten dazu kommen, dass der soeben detektierte Nulldurchgang von di/dt erneut detektiert wird. Infolge des Signalrauschens um den Nullwert kann der Nulldurchgang dabei auch mit umgekehrten Vorzeichen erfasst werden.
• Im Beispiel genügte eine Verringerung der minimalen Schrittweite auf dtMin=1e-7 s, um die sporadisch fehlerhafte Ereigniserkennung zu vermeiden:
  
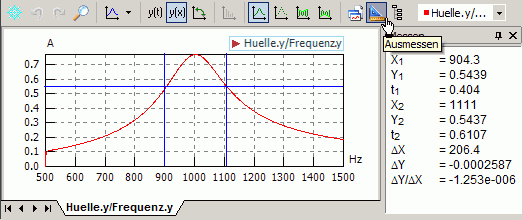
• Folgt man den Anweisungen im Fenster für das Ausmessen, so kann man problemlos an der Hüllkurve die erforderliche Absolutwerte und Differenzen zur Berechnung der Schwingkreisgüte ermitteln. Damit kann Frage 4 beantwortet werden.

Parallelschwingkreis

Mit den am Modell des Serienschwingkreises gewonnenen Erfahrungen werden wir nun ein neues Modell zur Bestimmung der Resonanzgüte eines Parallelschwingkreises aufbauen (Modell-Datei: Parallelschwingkreis.ism):

• Wir benutzen die gleichen Bauelemente, wie für den Serienschwingkreis. Den Drahtwiderstand verringern wir auf R=1 Ω.
• Die Spule bilden wir als Reihenschaltung von Induktivität L und Drahtwiderstand R nach.
• Anstatt mit einer Spannungsquelle erregen wir den Parallelschwingkreis mit einer Stromquelle.
• Im Resonanzfall ergibt sich ein Maximum der Spannungsmplitude über dem Kondensator. Da die Amplitude des Erregerstroms konstant bleibt, bedeutet dies, dass der Wechselstromwiderstand des Parallelschwingkreises im Resonanzfall am größten ist:

Frage 5:
Welche Kreisgüte Q ergibt sich bei einen Drahtwiderstand von R=1 Ω? Der aus aus der Simulation ermittelte Wert ist mit dem analytisch berechneten Wert zu vergleichen. Die Änderung der Kreisgüte im Vergleich zum höheren Drahtwiderstand des Serienschwingkreises ist zu erläutern.

Hinweise zur Lösung::

• Siehe http://de.wikipedia.org/wiki/Schwingkreis
• Für die analytische Berechnung der Kreisgüte

ist der "echte" Drahtwiderstand R_L zuvor in einen Ersatzwiderstand R_p umzurechnen:

← →