Software: CAD - Tutorial - Belastung - Vergleichsspannung
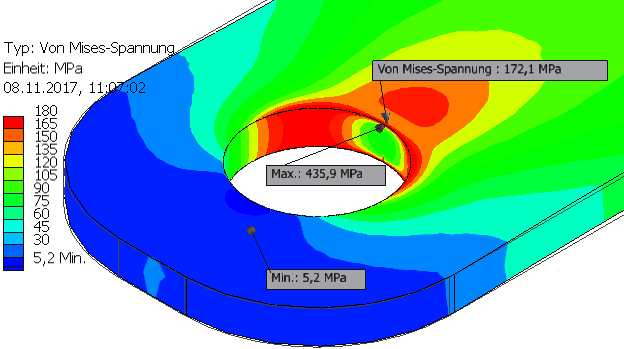
Nach der Simulation wird standardmäßig die berechnete mechanische Mises-Vergleichsspannung farblich codiert auf der Oberfläche des Bauteils als "Kontur-Darstellung" angezeigt. Die Farbskala ist dabei automatisch zwischen dem Minimal- und Maximal-Wert der Spannung linear skaliert.
Für das Bauteil wird der dreidimensionale Spannungszustand berechnet. Der Spannungszustand an einer beliebigen Position ist durch drei Normalspannungen (Spannung XX, Spannung YY und Spannung ZZ) sowie drei Schubspannungen (Spannung XY, Spannung YZ und Spannung XZ) definiert. Alternativ kann man jeweils eine dieser Spannungskomponenten als Kontur-Darstellung aktivieren (Häkchen im Browser).
Die Mises-Vergleichsspannung liefert aber meist schon hinreichende Aussagen in Bezug auf die Bauteilbelastung:
- Die maximale Vergleichsspannung basiert in der vorliegenden Implementierung auf der Bruchhypothese der maximalen Vergleichsspannung für dehnbare Materialien (von-Mises-Hencky-Theorie).
- Diese Theorie eignet sich für zähe, verformbare Materialien wie Aluminium, Bronze oder Stahl.
Hinweis:
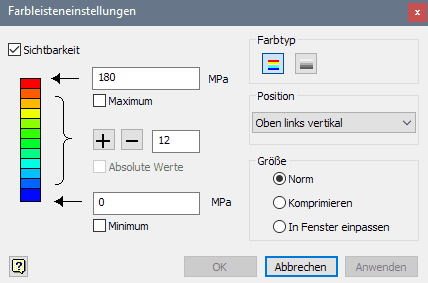
Die Grenzen der Farbleiste schränken wir auf einen sinnvollen Bereich ein. Die automatische Skalierung "verbrauchte" bereits über die Hälfte des Farbspektrums für den engen Bereich am Lochrand:
1. Überprüfung wertmäßig bekannter Spannungswerte:
- Abtasten der bekannten Punkte mittels Prüfen.
- So muss z.B. die Spannung in der Nähe der Last-Zugkraft entsprechend der Querschnittsfläche 100 MPa betragen.
2. Überprüfung der erwarteten Extrem-Bereiche:
- Da der Lochrand fixiert wurde, tritt die maximale Belastung am Loch in Zugrichtung auf. Die stärkste Belastung erfolgt dort direkt an den Kanten des Loches. Dort existiert der stärkste Gradient für die Verformung in Z-Richtung, weil sich die Dicke der Lasche durch die Zugkraft verringert, dies jedoch direkt am Loch wegen der Fixierung nicht möglich ist.
- Infolge der Nachgiebigkeit des Materials ist die Belastung auf der anderen Seite des Loches am geringsten. Das Material "fließt" praktisch um den Bolzen herum.
- Die berechneten Maximalwerte sind falsch, da sie vor allem aus den Idealisierungen der Befestigungsstelle resultieren!
- Die berechneten Minimalwerte nahe Null sind prinzipiell richtig.
3. Deutung von Besonderheiten:
- Im Beispiel wäre eine Besonderheit die leichte Spannungserhöhung am Rand des Bogens hinter dem Minimum. Erklärbar ist dies durch die Spannungen quer zur Zugrichtung, welche durch das "Fließen" des Materials um den Bolzen entstehen.
- Mysteriöser ist im Loch der Bereich geringerer Spannung innerhalb des maximal belasteten Bereiches. Erklärbar wird dies durch die Dickenänderung der Lasche infolge der Zugspannung. Die Dicke der Lasche kann sich an der Einspannung nicht ändern, was zusätzliche Spannungen am Lochrand "produziert".
Achtung: Die berechneten Ergebnisse darf man nie kritiklos akzeptieren!