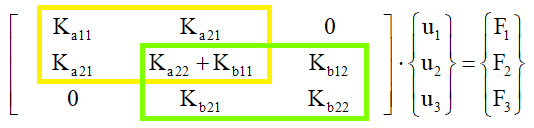Software: FEM - Tutorial - 2D-Bauteil - Elastostatische FE-Simulation

↑

← →

Elastostatische Finite-Elemente-Simulation (Grundlagen)

Nach über einhundert A4-Seiten Übungsanleitung haben wir nun ein Gefühl dafür erhalten:

1. dass man mittels Finite-Elemente-Simulation die Belastung eines mechanischen Bauteils analysieren kann,
2. dafür unterschiedliche Software und Modell-Ansätze nutzbar sind und
3. dass der Aufwand für den gesamten Analyse-Prozess von relativ gering bis extrem hoch reicht.

Abschließend zu diesem Einstieg in den Prozess der FEM-Analyse sollen nun die physikalisch-mathematischen Grundlagen auf einem qualitativen Niveau verdeutlicht werden:

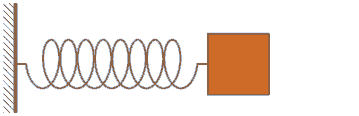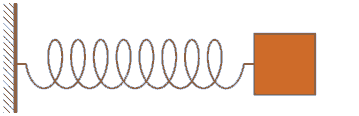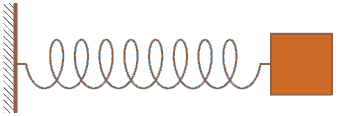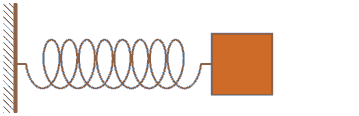
• Ausgangspunkt ist der reale Feder-Masse-Schwinger, der z.B. durch die Luft und die innere Reibung der Feder eine gewisse Dämpfung erfährt und den man durch eine äußere Kraft auf die schwingende Masse in seinem Verhalten beeinflussen kann:
  
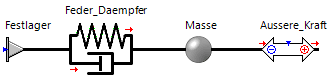
• Das reale Objekt "Feder-Masse-Schwinger" kann man durch idealisierte Elemente mit konzentrierten Parametern (z.B. Punktmasse, Feder, Dämpfer, Einspannung, Kraftquelle) schematisch nachbilden. Diese Reduktion auf "konzentrierte Elemente" gelingt gut, wenn die Bauteile selbst als Funktionselemente im Sinne dieser "konzentrierten Elemente" benutzt werden (z.B. Schraubenfedern, Stoßdämpfer, Massestücke):

• Anhand dieser mechanischen Analogie zu elektrischen Netzwerken ergibt sich die gewöhnliche Differentialgleichung des gedämpften Einmassen-Schwingers mit einem Freiheitsgrad der Bewegung:

m · ü + c · ú + k · u = f(t)

m    Masse 
ü    Beschleunigung (a=dv/dt) 
c    Dämpfung 
ú    Geschwindigkeit (v=du/dt) 
k    Steifigkeit (Federkonstante) 
u    Verschiebung (Auslenkung) 
f(t) zeitlich veränderliche Kraft 

Die Terme der Gleichung beschreiben 3 Kraftwirkungen, deren Summe mit der Erregung f(t) (der Last) im Gleichgewicht steht:

F_m= m·ü  → Trägheitskraft infolge Beschleunigung

F_c = c·ú   → Dämpfungskraft infolge Geschwindigkeit

F_k = k·u   → Rückstellkraft infolge Auslenkung

Wichtig:

• Die Bewegungsgleichung beschreibt nur die zeitabhängige Auslenkung der Masse und keine Position!
• Eine eindeutige Lösung der DGL für die zeitabhängige Position der Masse entsteht erst durch die Vorgabe der Position am masselosen Federende (z.B. in Form einer festen Einspannung).

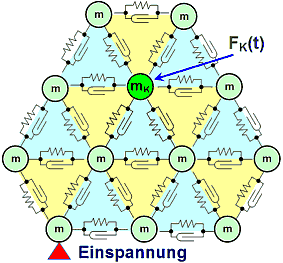
Im Unterschied zur Netzwerk-Methode mit konzentrierten Elementen wird bei der Finite-Elemente-Methode das Innere von mechanischen Bauteilen in extrem viele Massepunkte (Knoten) diskretisiert, welche wechselwirkend über die Steifigkeit und Dämpfung des dazwischenliegenden Materials (Elemente) verbunden sind. Es ergibt sich daraus die folgende Ersatzschaltung (Beispiel-Netz aus Dreieck-Elementen):

• Aus der Massedichte der Materialien und der Geometrie der Elemente ist die Masse eines jedes Elementes bestimmbar.
• Diese Elementmasse wird so auf die Knoten des Elements verteilt, dass für jedes Element die Summe aller Knotenmassen gleich der Elementmasse ist und die Teilmassen den gleichen gemeinsamen Schwerpunkt besitzen wie das Element.
• Werden Knoten von mehreren Elementen benutzt (der Normalfall), so ergibt sich ihre Masse als Summe aller anteiligen Elementmassen.
• Jeder Knoten ist über Feder-Dämpfer mit allen seinen Nachbarn verbunden (bei Viereck-Elementen verlaufen z.B. auch über die Viereck-Diagonalen Feder-Dämpfer).
• Die Steifigkeit (Federkonstante) einer diskreten Feder ergibt sich aus der Element-Geometrie und den Materialeigenschaften (E-Modul). Analog gilt dies für die diskreten Dämpfer.
• Kraftvektoren (Lastvektoren) greifen direkt an den einzelnen Knoten an und widerspiegeln den Einfluss der Netzumgebung (angedeutet mit F_K(t) an Knoten m_K).
• Randbedingungen bestimmen die Positionen oder Verschieblichkeitseinschränkungen einer Knoten-Teilmenge (angedeutet als "Einspannung" eines Knoten).

Die Bewegungsgleichung für den Einmassen-Schwinger begegnet uns nun verallgemeinert für Mehrmassen-Schwinger als Matrizen-Gleichung:

[M] · {ü} + [C] · {ú} + [K] · {u} = {F(t)}

[M]    Massenmatrix 
{ü}    Beschleunigungsvektor 
[C]    Dämpfungsmatrix 
{ú}    Geschwindigkeitsvektor 
[K]    Steifigkeitsmatrix 
{u}    Verschiebungsvektor mit jeweils den max. 6 Freiheitsgraden der Bewegung 
{F(t)} Kraftvektor (Lastvektor) 

Die Größe der Matrizen und Vektoren wird durch die Anzahl der Knoten des Netzes bestimmt.

Wichtig:

• Auch hier beschreiben die Bewegungsgleichungen nur die zeitabhängige Auslenkung aller Knoten und keine Positionen!
• Eine eindeutige Lösung der DGL für die zeitabhängige Position aller Knoten entsteht erst durch hinreichend viele Randbedingungen einer Knoten-Teilmenge (in Form von Positionsvorgaben oder zur Einschränkung der Verschieblichkeit)

Mit den vollständigen Gleichungen ist eine Simulation der wechselwirkenden Zustandsänderung jedes Knoten im Zeitbereich möglich (=dynamischer Modellansatz). Aus Gründen des Berechnungsaufwandes begnügt man sich meist mit stationärer (statischer) Berechnung, deren Vereinfachungen im Folgenden beschrieben werden:

• Modellansatz ohne Speicher für Bewegungsenergie (also ohne "Träge Masse").
• Kräftwirkungen, die nur bei zeitlichen Änderungen der Primär-Ergebnisse wirksam sind, werden nicht berücksichtigt (z.B. Dämpfer in der Mechanik).
• Die Last auf das Modell ist konstant.
• Berechnet wird der Endzustand (eingeschwungener Zustand) nach Aufbringen der Last (Elastostatische Simulation).
• Vom Einmassen-Feder-Schwinger bleibt nur noch die eingespannte Feder mit kontanter äußerer Kraft übrig → reduzierte "Bewegungsgleichung" k · u = F:

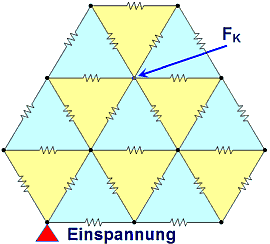
• In Analogie dazu reduziert sich für die Strukturmechanik das Finite-Elemente-Modell auf ein Netz von Steifigkeiten zwischen den (masselosen) Knoten:
  

mit der zugehörigen reduzierten Matrizen-Gleichung:

[k] · {u} = {F}

Bei der FEM-Belastungsanalyse muss man unterscheiden zwischen Primär- und Sekundär-Ergebnissen. Wir betrachten formelmäßig dabei nur noch den statischen Fall:

1. Primär-Ergebnisse werden direkt bei der Lösung des Gleichungssystems ausgerechnet, dass sind die:
   • Verschiebungen aller Knoten in Bezug auf den unbelasteten Zustand:

   Für das eindimensionale Feder-System wird dazu die Bewegungsgleichung nach der Verschiebung u umgestellt:
   u = F · k ^-1

   Analog dazu ist für das statische Finite-Elemente-Modell die Umstellung des Gleichungssystems nach dem Verschiebungsvektor {u} erforderlich:
   {u} = {F} · [K]^-1 ← die Steifigkeitsmatrix muss invertiert werden.

2. Sekundär-Ergebnisse werden auf der Grundlage der Primär-Ergebnisse berechnet:
   • Absolute Positionen aller Knoten aus der Summe der Knoten-Positionen des unbelasteten Zustands und der Knoten-Verschiebungen im belasteten Gleichgewichtszustand.
   • Haupt- und Vergleichsspannungen in den Knoten bzw. den Gausspunkten sowie deren Interpolation über das Finite-Element.
   • Lagerkräfte (Auflagereaktionen)

Steifigkeitsmatrix

Steifigkeitsmatrizen spielen eine zentrale Rolle innerhalb der Finite-Elemente-Methode. Deshalb sollen ihre physikalische Bedeutung und ihre formelle Bildung im Folgenden qualitativ etwas näher betrachtet werden:

• Eine Steifigkeitsmatrix enthält die Zahlenwerte, welche die Steifigkeit aller Elemente in der betrachteten, diskretisierten Geometrie repräsentieren.
• Man kann sich das stark vereinfacht als diskrete Federn zwischen allen Element-Knoten jeweils eines Elements vorstellen (Siehe Bild oben).
• Ein Element-Knoten kann maximal 6 Freiheitsgrade der Bewegung besitzen (3 translatorisch / 3 rotatorisch). Für jeden Freiheitsgrad ist ein "Feder"-Steifewert erforderlich (eine "separate Feder").
• Alle Knoten einer Steifigkeitsmatrix müssen die gleiche Art und Anzahl von Freiheitsgraden besitzen. Dies ist bei der Auswahl der zu vernetzenden Elemente zu berücksichtigen.
• Die Matrixgröße ist (P·n) x (P·n) mit P=Knotenzahl / n=Anzahl der Freiheitsgrade.

Bei einem Bauteil-Modell muss man grundsätzlich unterscheiden zwischen den Element-Steifigkeitsmatrizen und der Gesamt-Steifigkeitsmatrix:

1. Element-Steifigkeitsmatrizen (in lokalen Element-Koordinaten)

Für das Berechnen aller Knoten-Verschiebungen mit Ihren jeweils maximal 6 Freiheitsgraden wird als Grundlage die sogenannte Gesamt-Steifigkeitsmatrix [K] benötigt:

{u} = {F} · [K]^-1

• Zur Bildung dieser Gesamt-Steifigkeitsmatrix wird in einem ersten Schritt für jedes Element eine Element-Steifigkeitsmatrix innerhalb seines lokalen Element-Koordinatensystem erstellt.
• Solch eine "normierte" Element-Steifigkeitsmatrix enthält die Zahlenwerte, welche die Steifigkeit des Elements repräsentieren.
• Die Anzahl der Freiheitsgrade (1...6) der Element-Knoten innerhalb ihres lokalen Element-Koordinatensystems ist durch den Element-Typ vorgegeben.
• Element-Knotenzahl P_e und Freiheitsgrade n_e der Knoten ergeben Elementtyp-abhängig eine Matrixgröße (P_e·n_e) x (P_e·n_e)

Die Zahlenwerte einer Element-Steifigkeitsmatrix werden aus den Abmessungen des Elementes und seinen Materialdaten berechnet:

• Für ein Stab-Element (also ein gerades strichförmiges Element zwischen 2 Knoten als einfachster Fall) gehen in die Element-Steifigkeitsmatrix die Länge, die Querschnittsfläche und die Materialdaten (der Elastizitätsmodul) des Elements ein.
• Für ein Balken-Element gehen in die Element-Steifigkeitsmatrix zusätzlich die Widerstandsmomente gegen Biegung und eventuell gegen Verdrehung entsprechend der Querschnittsform ein.
• Für ebene Elemente und räumliche Elemente gilt dies analog, es bedarf jedoch eines wesentlich komplexeren Formelapparates.
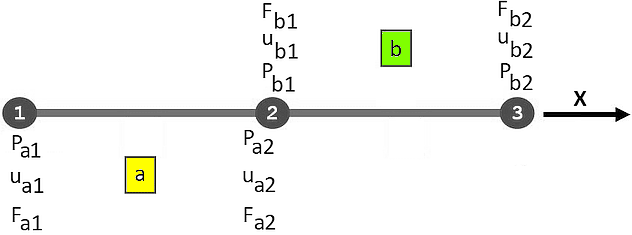
• Beispiel: zwei verbundene 1D-Stabelemente (Knotenverschiebung nur in X-Richtung):

• Unabhängig voneinander ergeben sich die beiden Element-Steifigkeitsmatrizen für die elastostatischen Bewegungsgleichungen innerhalb der lokalen Koordinatensysteme:

2. Element-Steifigkeitsmatrizen (in globalen Bauteil-Koordinaten)

Im nächsten Schritt werden die normierten Element-Steifigkeitsmatrizen in das globale Koordinatensystem des Bauteils transformiert:

• Die erforderlichen Verschiebungen und Drehungen jedes Elements bis zu seiner korrekten Position führen zu modifizierten Werten in seiner Element-Steifigkeitsmatrix.
• Die Dimension (1D, 2D, 3D) des globalen Systems muss mit der Dimension der Elemente übereinstimmen! Dies ist bereits bei der Auswahl der zu vernetzenden Elemente zu berücksichtigen.
• Für das einfache Beispiel der 1D-Stabelemente bleiben durch die Positionsänderungen im globalen 1D-Koordinatensystem die Werte erhalten!

3. Gesamt-Steifigkeitsmatrix

Die Gesamt-Steifigkeitsmatrix erstreckt sich über alle Knoten des Gesamt-Modells mit ihrem einheitlichen Freiheitsgrad n_G:

• Unabhängig von der lokalen Knoten-Nummerierung in den Elementen erfolgt eine Nummerierung aller Knoten des Gesamt-Modells von 1...P_G (im Beispiel Knoten 1...3 mit zugehörigen Verschiebungen und Kräften).
• Zusammen mit dem Freiheitsgrad n_G ergibt dies die Größe der Gesamt-Steifigkeitsmatrix zu (P_G·n_G) x (P_G·n_G)
• Nach dem Anlegen dieser Matrix können alle Elemente den Anfangswert=0 erhalten.
• In einem nächsten Schritt wird eine Zuordnung aller Element-Knoten zu den Modell-Knoten vorgenommen.
• Ergibt sich dadurch eine Wechselwirkung zwischen Modell-Knoten, so können zu den zugehörigen Matrix-Elementen die Steifigkeitswerte aus der Element-Steifigkeitsmatrix hinzu addiert werden.
• Überlappen sich Elemente mit mindestens zwei Knoten, so repräsentiert die Summenbildung in der Gesamt-Steigkeitsmatrix praktisch eine "Parallelschaltung von Federn".

← →