Software: FEM - Tutorial - Formoptimierung - Methode der Zugdreiecke: Unterschied zwischen den Versionen
| Zeile 43: | Zeile 43: | ||
#* Nach dem gleichen Prinzip könnte man iterativ weitere Zugdreiecke ergänzen und damit einen immer stetigeren Übergang in den "Stamm" realiseren. | #* Nach dem gleichen Prinzip könnte man iterativ weitere Zugdreiecke ergänzen und damit einen immer stetigeren Übergang in den "Stamm" realiseren. | ||
#* Wir beenden die Konstruktion jedoch mit dem dritten Dreieck, weil danach keine praktischen Verbesserungen für die Spannungshomogenisierung mehr spürbar sind! | #* Wir beenden die Konstruktion jedoch mit dem dritten Dreieck, weil danach keine praktischen Verbesserungen für die Spannungshomogenisierung mehr spürbar sind! | ||
#* '''''Hinweis'':''' Die Breite des Bauraums setzen wir vorläufig auf einen relativ großen Wert '''B=10 mm''', um insbesondere bei noch folgenden Abrundung die Übersicht zu behalten. Mit diesem Maß muss die Skizze vollständig bestimmt sein! | #* '''''Hinweis'':''' Die Breite des Bauraums setzen wir vorläufig auf einen relativ großen Wert '''B=10 mm''', um insbesondere bei der noch folgenden Abrundung die Übersicht zu behalten. Mit diesem Maß muss die Skizze vollständig bestimmt sein! | ||
=== Ersatz durch eine Kreisbogen-Kontur === | === Ersatz durch eine Kreisbogen-Kontur === | ||
Aktuelle Version vom 10. Juli 2019, 13:43 Uhr
Vorbemerkungen
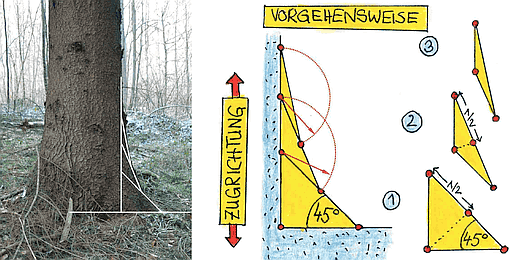
Wie wir in unserer vorherigen Belastungsstudie gesehen haben, ist eine Verringerung der Kerbspannung durch Abrundung der Kerbe erwartungsgemäß möglich. Jedoch erfordert die reine Abrundung sehr viel Bauraum, um einen kleinen Kerbfaktor zu erhalten. Im Folgenden soll am Beispiel der Methode der Zugdreiecke gezeigt werden, wie Material-effektiv die Natur durch die evolutionäre "Erfindung" der biologischen Wachstumsregel zu ähnlichen bzw. besseren Ergebnissen in Hinblick auf die Festigkeit einer Kerbe kommt (Bild aus einem "Mattheck-Poster"):
Der Hebelarm unserer Tast-Sonde entspricht dem Baumstamm und der Einspannbereich entspricht dem Wurzelballen im Erdreich (Ausgangsdatei "Sonde_xx.ipt"):
Das einleitende Bild zeigt die Methode der Zugdreiecke in qualitativer Form. Um jedoch ein optimales Ergebnis zu erreichen, benötigt man noch zwei wesentliche Informationen:
- Wie weit entfernt von der Kerbe muss man mit dem ersten Zugdreieck beginnen?
- In welchem Maße muss man die stumpfen Winkel an den Zugdreiecken abrunden?
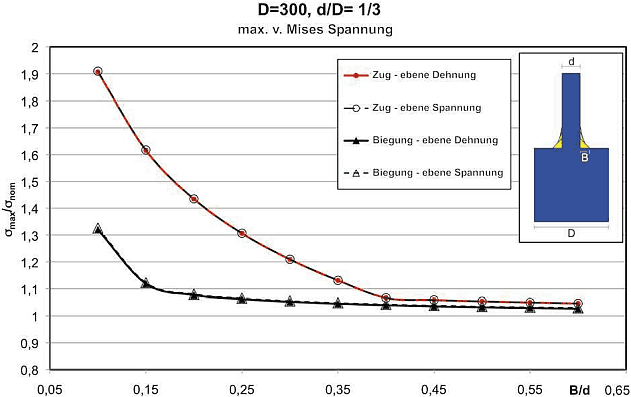
Hierfür wurden systematische Untersuchungen mittels der FEM-Analyse für den vereinfachten ebenen Fall durchgeführt, die wir als Grundlage für unsere Konstruktion verwenden können:
1. Seitlicher "Bauraum" B
Die Berechnungen erfolgten zwar mit konkreten Maßen und Material-Kennwerten, aber auf Grund der linearen Simulation können die Ergebnisse verallgemeinert werden:
- Es wird davon ausgegangen, dass sich die Länge B der Grundseite des ersten Zugdreiecks proportional zum "Stammdurchmesser" d ändern muss.
- Die Breite D des Einspannbereiches (für das "Wurzelwerk") sollte ca. 3x so groß wie der "Stammdurchmesser" d sein.
- Insbesondere für Zugbelastung (wie bei unserer Sonde) sollte im gezeigten Beispiel das Verhältnis von B/d=0,4 für einen minimal möglichen Kerbspannungsfaktor bei möglichst kleinem Bauraum betragen:
- Infolge abweichender Material-Kennwerte wird bei unserer Tast-Sonde das optimale B/d-Verhältnis einen etwas anderen Wert besitzen. Wir nutzen für eine grobe Anfangsnäherung trotzdem diesen Wert B/d=0,4:
- Die Höhe unseres Sonden-Hebels kann mit dem Stammdurchmesser d = 3 mm gleichgesetzt werden.
- Damit ergibt sich ein minimales B = 1,2 mm.
2. Abrundung der stumpfen Winkel zwischen den Dreiecken
Fertigungstechnisch ist es günstig, eine gekrümmte Kontur als "knickfreie" Aneinanderreihung von Kreisbogen zu beschreiben:
- Die ursprüngliche rechteckige Kerbe ist nach Konstruktion der Zugdreiecke durch einen stumpfwinkligen Streckenzug gefüllt.
- Die Knicke im Konturverlauf der Kerbe sind sowohl fertigungstechnisch, als auch belastungsmäßig ungünstig.
- Deshalb sollte dieser Streckenzug durch Kreisbogen mit passenden Radien ersetzt werden, welche knickfrei ineinander übergehen.
Konstruktion der Zugdreieck-Kontur
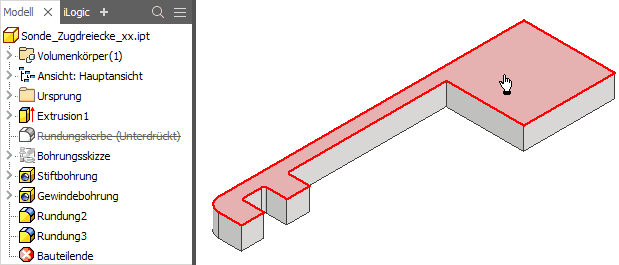
Von unserer Ausgangsdatei "Sonde_xx.ipt"erzeugen wir im Autodesk Inventor mittels "Speichern unter" eine Datei "Sonde_Zugdreiecke_xx.ipt" im aktuellen Projekt-Ordner. Diese bildet die Grundlage für die Formoptimierung der Kerbe mittels der Methode der Zugdreiecke:
- Die Rundungskerbe als Element unterdrücken wir (Kontextmenü) und erzeugen danach eine neue Skizze für die Konstruktion der Zugdreiecke auf dem Bauteil:
Innerhalb dieser Skizze konstruieren wir schrittweise die optimierte Kerb-Kontur:
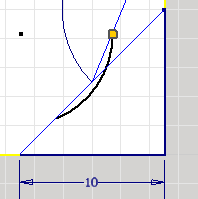
- Basisdreieck (45°-gleichschenklig in 90°-Kerb-Ecke):
- Beim Zeichnen des Dreiecks direkt in der Ecke unter Ausnutzung der automatisch erzeugten Abhängigkeiten werden auch die beiden Eck-Kanten automatisch in die Skizze projiziert.
- Das gibt Probleme beim Auswählen übereinander liegender Linien, welches dann mittels "Kontextmenü > Andere auswählen ..." erfolgen muss (z.B., um die Abhängigkeit "gleich" für beide Dreieckseiten zu definieren).
- Die Breite B lassen wir vorläufig unbemaßt ("1 Bemaßung erforderlich" in der Statuszeile bedeutet im Beispiel, dass man die Größe des Dreiecks durch Ziehen mit dem Cursor an einer Ecke noch ändern kann → Bitte Testen!).
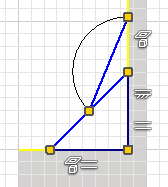
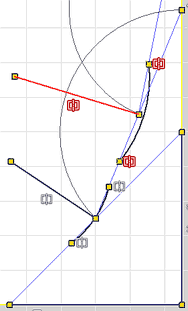
- Zweites Dreieck (auf halber Basisdreieck-Hypotenuse):
- Mittels MFL > Erstellen > Bogen durch Mittelpunkt konstruieren wir nur die Kerbkontur-Seite des zweiten Dreiecks als Linie zwischen den Endpunkten des Bogens:
- Hinweis: Zur besseren Unterscheidung der Linien- und Bogen-Elemente wurden deren Farben und Strichstärken teilweise mittels Kontextmenü > Eigenschaften geändert.
- Der Freiheitsgrad=1 muss erhalten bleiben → Testen durch Größenänderung mittels Cursor!
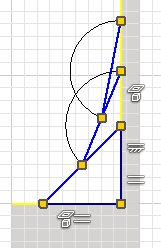
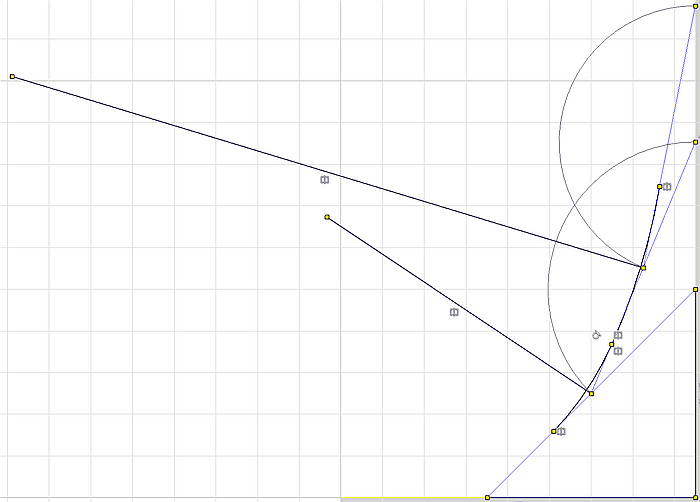
- Letztes Dreieck (nach gleichem Prinzip):
- Nach dem gleichen Prinzip könnte man iterativ weitere Zugdreiecke ergänzen und damit einen immer stetigeren Übergang in den "Stamm" realiseren.
- Wir beenden die Konstruktion jedoch mit dem dritten Dreieck, weil danach keine praktischen Verbesserungen für die Spannungshomogenisierung mehr spürbar sind!
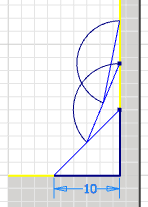
- Hinweis: Die Breite des Bauraums setzen wir vorläufig auf einen relativ großen Wert B=10 mm, um insbesondere bei der noch folgenden Abrundung die Übersicht zu behalten. Mit diesem Maß muss die Skizze vollständig bestimmt sein!
Ersatz durch eine Kreisbogen-Kontur
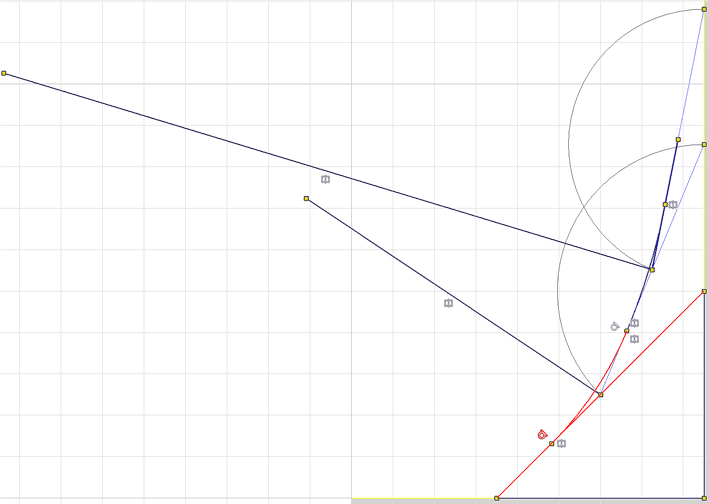
Der Knick zwischen Basis-Dreieck und Einspann-Bereich hat spannungsmäßig keine Auswirkung, weil der Kraftfluss vom "Stamm" schon vorher in den "Boden" geht. Alle stumpfen Winkel vom 2. Dreieck an aufwärts ersetzen wir jedoch durch Kreisbogen, um dort die Kerbwirkung zu mindern:
- Dabei wird die gesamte Streckenkontur als Folge von Kreisbogen beschrieben, welche möglichst ohne Knick ineinander übergehen.
- Damit sich die zu konstruierenden Kreisbogen vom Rest der Skizze abheben, versehen wir zuerst alle Kerbkontur-Linien der Dreiecke mit der Eigenschaft "Linienstärke 0 mm".
- Der Radius zum Mittelpunkt des Kreisbogens soll die Winkelhalbierende des jeweiligen stumpfen Winkels bilden. Der Kreisbogen zum Abrunden des stumpfen Winkels soll sich symmetrisch um diese radiale Linie erstrecken.
- Wir beginnen mit dem Kreisbogen am stumpfen Winkel zwischen Basisdreieck und 2. Dreieck:
- Mittelpunkt irgendwo ungefähr mittig zum stumpfen Winkel
- 1. Bogenpunkt auf 1. Schenkel des Winkels
- 2. Bogenpunkt in die Nähe des 2. Schenkels -> Bogen ok
- Abhängigkeit "Koinzident" zwischen 2. Bogenpunkt und 2. Schenkel
- Linie zwischen Bogen-Mittelpunkt und Scheitelpunkt des stumpfen Winkels
- Abhängigkeit "Symmetrisch" zwischen 1. und 2. Bogenpunkt zu dieser Symmetrielinie:
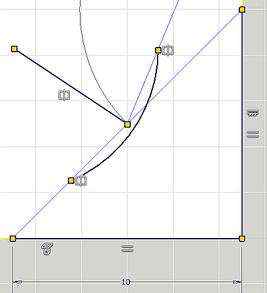
Die Länge des Bogens kann man nun mit dem Cursor ändern. Damit vorerst keine Überdeckung mit dem nächsten Bogen stattfindet, sollte die Länge kürzer sein, als die halbe Hypotenuse des Basisdreiecks.
- Für den stumpfen Winkel zwischen 2. und 3. Dreieck konstruieren wir einen Kreisbogen nach dem gleichen Prinzip.
- Bevor wir beide Bogen verbinden, müssen wir ihre Radien soweit vergrößern, dass die Bogen innerhalb der stumpfen Winkel liegen (Ziehen mit dem Cursor am Mittelpunkt).
- Danach können wir die beiden Endpunkte der Bogen mittels der Abhängigkeit "Koinzidenz" verbinden.
- Mittels der Abhängigkeit "Tangential" gewährleisten wir einen knickfreien Übergang zwischen beiden Bogen. Falls bei der Definition der Tangential-Abhängigkeit eine Fehlermeldung wegen Überbestimmtheit erscheint, so ist zumindest 1 Radius noch zu kurz und der zugehörige Bogen deshalb noch nicht innerhalb des stumpfen Winkels.
- Zur Kontrolle: Nach dem Verbinden der Bogen mit tangentialen Übergang sollte die Skizze noch 2-fach unbestimmt sein (noch 2 Maße erforderlich):
- Hinweis: Die fehlenden 2 Abhängigkeiten müsste man eigentlich durch 2 Tangentialabhängigkeiten jeweils zwischen Bogen und der anschließenden Dreieckseite ergänzen. Nur dadurch erhält man einen perfekten knickfreien Auslauf der beiden Kreisbogen. Leider streikt Autodesk Inventor bei der jeweils zweiten Tangentialabhängigkeit, weil diese schon fast erfüllt ist und damit die Skizze angeblich überbestimmt würde.
- Wir lassen deshalb den oberen Bogen auf der Mitte des "Radius" der obersten Dreieckseite enden. Dazu benötigen wir eine zusätzliche Linie entlang des "Radius", auf der wir den erforderlichen Mittelpunkt fangen können:
- Über die Abhängigkeit "Koinzidenz" verbinden wir den Mittelpunkt dieser Hilfslinie mit dem Endpunkt des oberen Abrundungsbogens.
- Den Endpunkt des unteren Abrundungsbogens lassen wir mittels der Abhängigkeit "Tangential" knickfrei in die Hypotenuse des Basisdreiecks übergehen.
- Danach ist die Skizze vollständig bestimmt und es fehlt nur noch ein Kreisbogen für den Knick zum Tast-Hebel:
- Diesen Kreisbogen konstruieren wir nach dem ähnlichem Prinzip, indem wir das eine Bogenende direkt am Ende der "Radius"-Hilfslinie befestigen und das andere Ende auf der Kante des Tast-Hebels. Die Hilfslinie zwischen Mittelpunkt und Scheitelpunkt ist nicht erforderlich!
- Danach gewährleisten wir an beiden Enden des neuen Bogens mittels Tangential-Abhängigkeit einen knick-freien Übergang zu den geraden Linien:
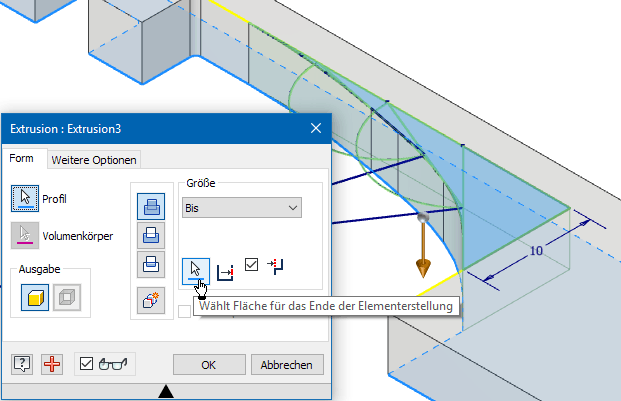
- Nach Fertigstellen der Skizze kann man mittels MFL > Extrusion das konstruierte und abgerundete Zugdreieck-Profil markieren und dann die Extrusion bis zur gegenüberliegenden Seite durchführen (unbedingt auch alle schmalen Teilflächen erfassen!):
- Achtung: Erst nach der Extrusion ändern wir in der Skizze die Breite B auf den abgeschätzten Minimalwert von 1,2 mm.
Analyse und Dimensionierung der Kerbe
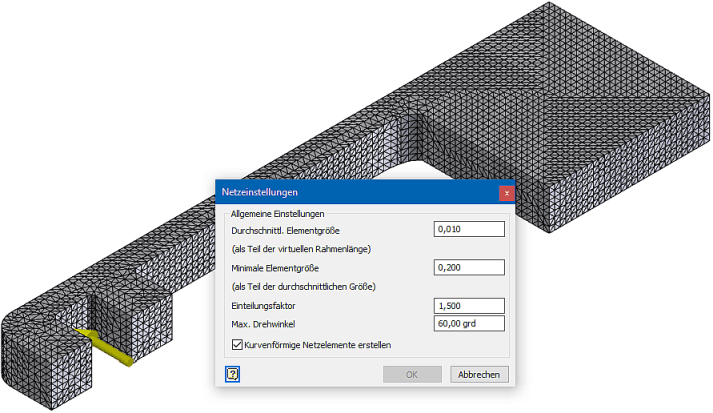
Es ist für das Beispiel nicht erforderlich, in den Kerben eine lokale, feinere Vernetzung vorzunehmen, deshalb können die vorhanden lokalen Vernetzungen gelöscht werden. Es genügt eine hinreichend feine globale Vernetzung, mit dem Ziel, die Simulationzeit kurz zu halten:
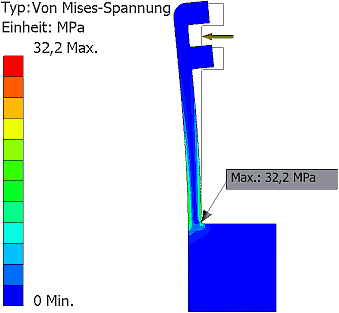
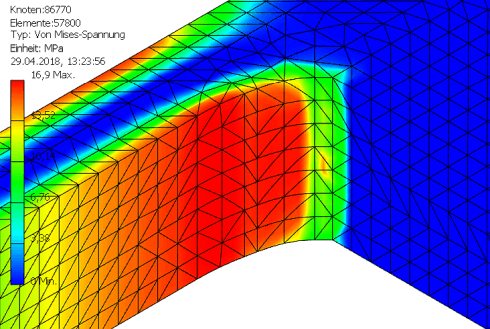
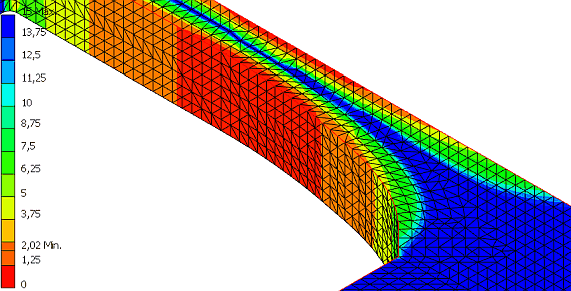
Im Ergebnis ergibt sich bei der minimal sinnvollen Baubreite von B=1,2 mm mit der Methode der Zugdreiecke ungefähr eine Halbierung der maximalen Kerbspannung im Vergleich zur Abrundung mit r=0,5 mm:
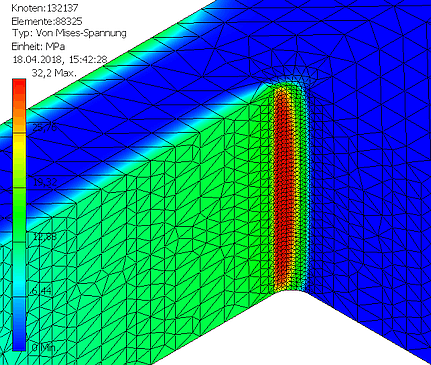
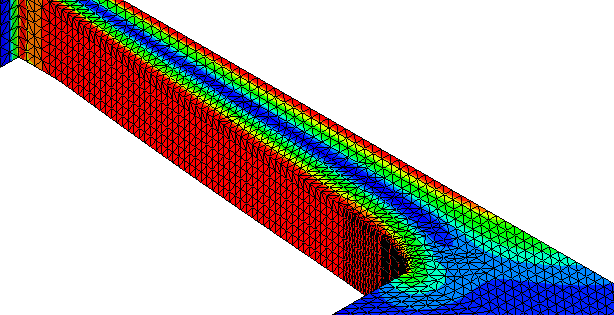
Die quantitative Verbesserung klingt nicht spektakulär. Aber qualitativ ergibt sich ein völlig anderes Bild, weil durch die Methode der Zugdreiecke eine Homogenisierung des Spannungsverlaufs erfolgt. Deshalb hier im Vergleich nochmal der Spannungsverlauf bei einfacher Abrundung:
Hinweise:
- Zur Erreichung des angestrebten Sicherheitsfaktors ist nach entsprechender Kerbform-Optimierung nicht die Kerbe selbst die Schwachstelle, sondern die Einspannseite des Tast-Hebels.
- Dies erkennt man auch an der hohen Belastung auf der Hebel-Oberseite über der Kerbe.
- Wie bereits bei der Anpassung des Rundungsradius beheben wir die Schwachstelle durch eine leichte Verdickung dieses Hebelabschnitts, indem wir die Zugdreieck-Kerbform entsprechend groß wählen (Bild zeigt Sicherheitsfaktoren entlang des Hebels):
- Leider steht im Rahmen dieser Übung keine Software zur Verfügung, mit welcher eine Formoptimierung z.B. mit dem CAO-Verfahren vorgenommen werden kann. Damit würde im Beispiel eine extreme Homogenisierung der Spannung auf der Unterseite des Tasthebels (einschließlich der Kerbe) erreicht. Das folgende Bild zeigt den Verlauf der von Mises-Spannung im Ergebnis eines für ein 2D-FEM-Modell selbst geschriebenen ANSYS-Optimierungsscripts (Autor Dr.-Ing. Jens Schirmer) :
- Insbesondere im Bereich der Kerbe ist damit wesentlich weniger Bauraum erforderlich, weil die Optimierung der einzelnen Hebel-Abschnitte unabhängiger voneinander erfolgen kann!
Frage 3
Zugdreieck-Breite B für Sicherheitsfaktor ≥ 2 im gesamten Bauteil:
a) Wie groß muss die Baubreite B an der kritischen Kerbe mindestens gewählt werden?
b) Wie groß ist damit der minimale Sicherheitsfaktor außerhalb der Kerbe?