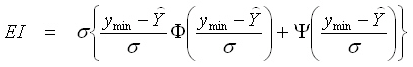Software: FEM - Tutorial - Magnetfeld - C-Kennfeld Adaptiver Gauss-Prozess

↑

← →

Adaptiver Gauß-Prozess

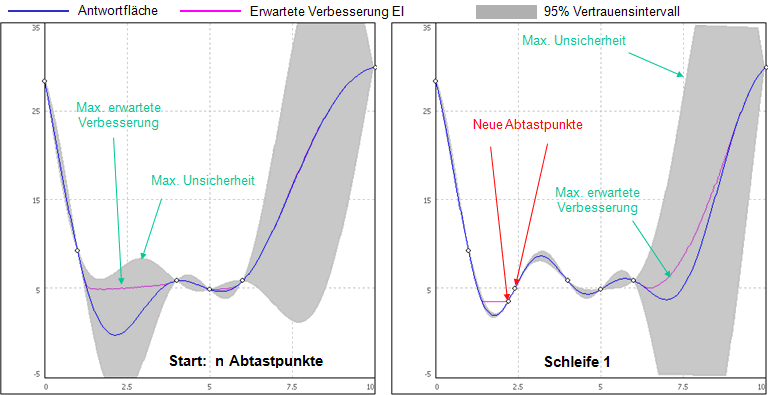
Der adaptive Gauss-Prozess soll genutzt werden, um ausgehend von einer vorhandenen Stichprobe mit möglichst wenigen zusätzlichen Stützstellen ein hochwertiges Ersatzmodell zu gewinnen. Dabei werden ausgehend von den vorhandenen Abtastpunkten nach Identifikation der Antwortflächen die Positionen der maximalen Unsicherheit und der maximal zu erwartenden Verbesserung ermittelt. Dort werden mit dem Modell zwei neue Stützstellen berechnet:

Dieser Prozess wird iterativ ausgeführt (bis max. Stützstellen-Zahl oder geforderte Genauigkeit erreicht):

Adaptiver Gauß-Prozess:

• Die erwartete Verbesserung EI entspricht dem Potenzial zur Verbesserung der Approximationsgüte. Sie ist definiert mit
  
  wobei Φ und ψ die Verteilungsfunktion und die Dichtefunktion der normalisierten Normalverteilung sind.
• Der adaptive Gauß-Prozess schlägt für die nächste Schleife der Modellberechnungen weitere Punkte im Entwurfsraum vor, welches folgende Bedingungen erfüllen:
  1. Maximierung der erwarteten Verbesserung, um den optimalen Entwurf in Hinblick auf die geforderte Genauigkeit zu validieren.
  2. Maximierung der Varianz σ, um die Unsicherheiten der Vorhersage zu minimieren.
• Diese nächsten Punkte werden anhand des aktuellen Gauß-Prozess-Ergebnisses durch Optimierung mittels einer Evolutionsstrategie berechnet.

Konfiguration

Durch Duplizieren des Experiments "Kennfeld-Identifikation" gewinnen wir ein neues Experiment "Kennfeld-adaptiv":

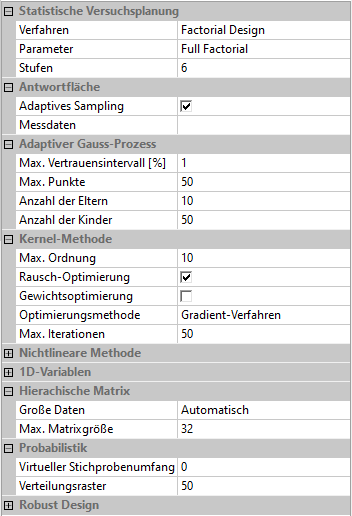
• Basis ist wieder ein 6-stufiges Full Factorial Design, dessen Ergebnis-Antwortfläche durch zusätzliche Abtastungen des Modells verbessert werden soll.
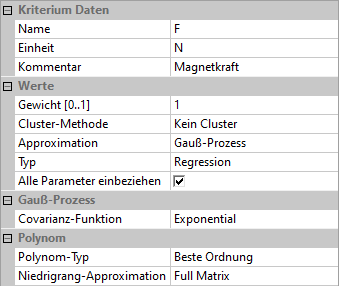
• Für die Polynom-Ordnung und für die Covarianz-Funktion nutzen wir diesmal jedoch nicht die Automatismen, sondern legen auf Basis der gesammelten Erfahrungen eine niedrige Polynom-Ordnung und eine "gutmütige" Covarianz-Funktion fest. Als günstig für den Gauß-Prozess der beiden Antwortflächen (F und Psi) haben sich die einheitliche Polynomordnung=1 mit der Co-Varianzfunktion=Exponential bewährt und diese sollten deshalb hier verwendet werden:

• Wir aktivieren in der Versuchsplanung des adaptive Sampling und blenden mittels "Standardparameter=False" die Standardeinstellungen ein.
• Immer ausgehend vom Ergebnis des aktuellen Gauß-Prozesses sollen dann durch den adaptiven Gauß-Prozess die nächsten erforderlichen Stützstellen berechnet werden.
• Sowohl für den Gauß-Prozess als auch für den sich anschließenden adaptiven Gauß-Prozess verwenden wir eine Evolutionsstrategie mit einheitlichen Vorgabewerten von 10 Eltern und 50 Kindern.
• Die angestrebte Genauigkeit der Approximation wird durch das max. Vertrauensintervall (im Beispiel 1%) beschrieben.
• Die Anzahl der max. Punkte=50 dient als vorzeitiges Abbruch-Kriterium, falls die geforderte Genauigkeit noch nicht erreicht wurde. Diese Anzahl umfasst nur die neu vorgeschlagenen Punkte nach dem ersten Gauß-Prozess und ist in der Trial-Version auf 100 Punkte begrenzt.

Fortschritt

• Um den Fortschritt der adaptiven Kennfeld-Approximation Live verfolgen zu können, schalten wir vorläufig "Adaptives Sampling=False".
• Damit findet nach Start des Experiments nur für die 36 Punkte des Full Factorial Design eine Approximation mittels "normalem" Gauß-Prozess statt.
• Hierfür konfigurieren wir die folgenden grafischen Darstellungen:

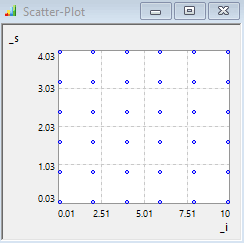
  2D Anthill-Plot (_i,_s):

  

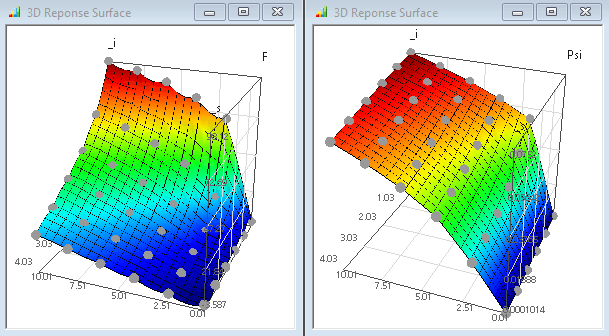
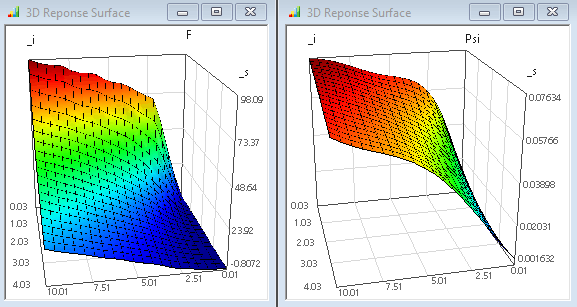
  3D-Antwortflächen:

  

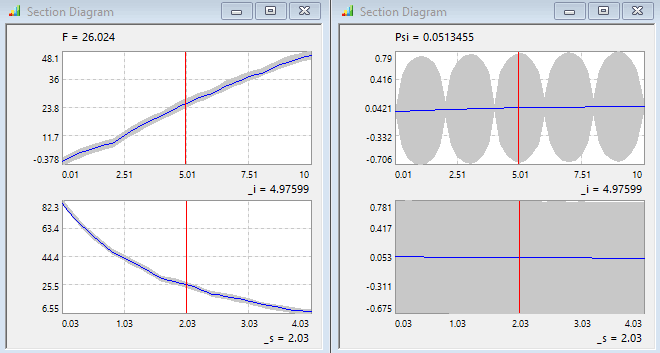
  Schnittdiagramme:

  

Adaptiver Gauß-Prozess:

• Nach erfolgreicher Initialisierung und Visualisierung der Ausgangslösung aktivieren wir wieder "Adaptives Sampling=True"
• Neuberechnen der Antwortflächen startet dann den iterativen adaptiven Gauß-Prozess und ergänzt in jeder Iteration zwei weitere Punkte.
• Unter Einbeziehung dieser zwei neuen Punkte wird dann der "normale" Gauß-Prozess berechnet und visualisiert. So kann man Live diesen Approximationsprozess beobachten.
• Hinweis:
  • Leider funktioniert die Beobachtung des Approximationsfortschrittes in der aktuellen OptiY-Version nur sehr eingeschränkt.
  • Bei genauem Hinschauen erkennt man, dass jeweils zwei neue Stützstellen mit dem Modell berechnet werden.
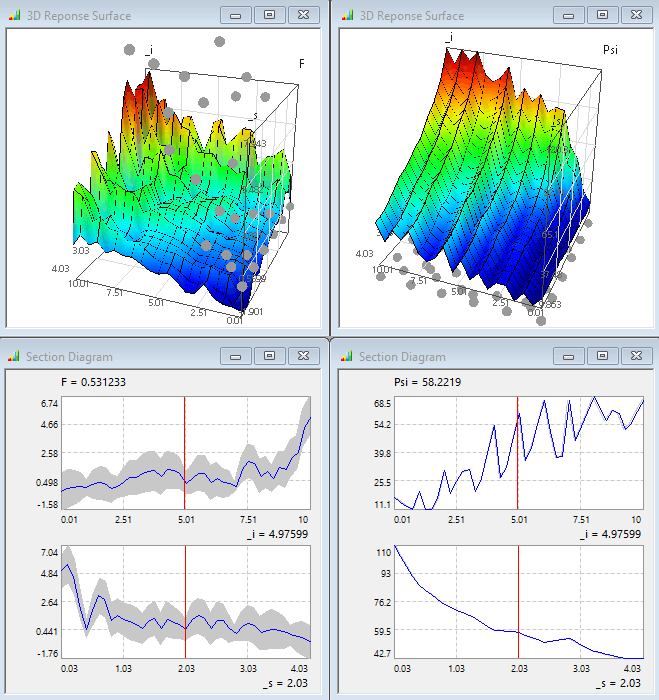
  • Daraus ergeben sich jedoch jeweils sehr wellige Antwortflächen, welche kein sinnvolles Zwischenergebnis widerspiegeln:

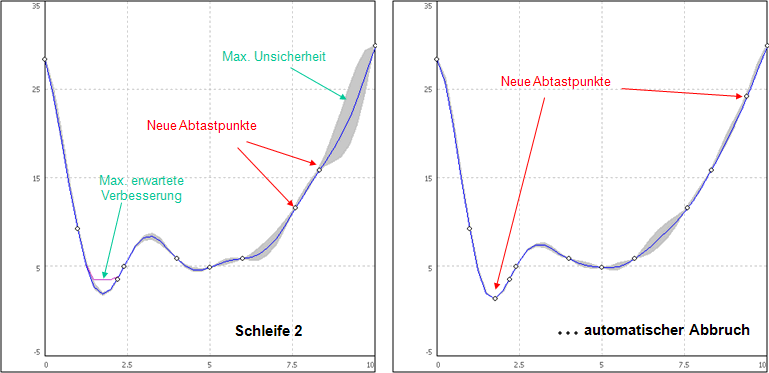
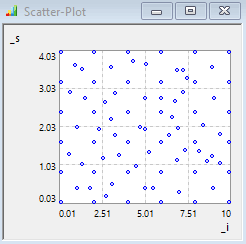
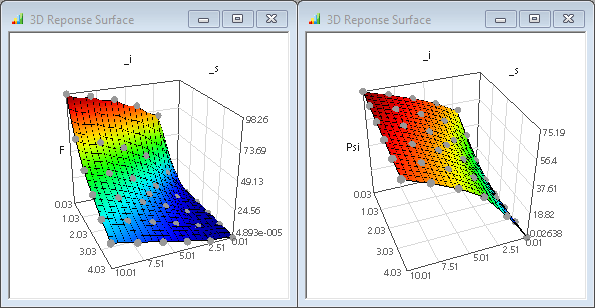
Die zusätzlichen Abtaststellen verteilen sich weitestgehend gleichmäßig über den gesamten Streubereich:

• Der Abbruch erfolgte im Beispiel nach Erreichen der max. zusätzlichen Punkteanzahl (also vor dem Erreichen der geforderten Genauigkeit). Die dann korrekt berechneten Antwortflächen zeigen jedoch noch physikalisch nicht begründbare Welligkeiten, negative Werte und "Knicke":

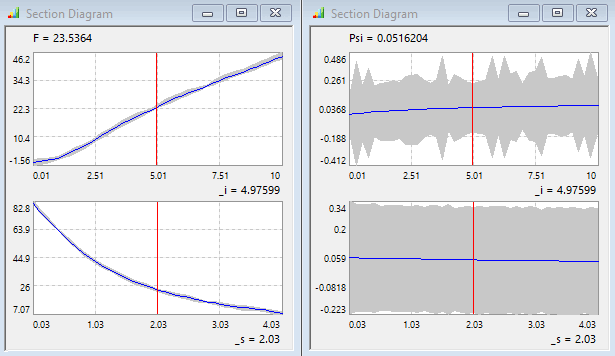
• Das 95%-Erwartungsintervall verringerte sich für beide Ersatzfunktionen im Vergleich zur Ausgangslösung:
  

Fazit

Der adaptive Gauß-Prozess verbessert schrittweise die Qualität eines Ersatzmodells ausgehend von der möglichst kleinen globalen Abtastung des zu berücksichtigenden Werte-Bereiches (hier 6-stufiges Full Factory Design, um eine qualitativ bereits anschauliche Ersatzfunktion zu erhalten):

• Mit wenig Vorwissen zum Verlauf der realen Antwortfläche erhält man bei einer hinreichend großen maximal zulässigen Punkte-Anzahl eine glaubwürdige Approximation auch an kritischen Stellen einer nichtlinearen Übertragungsfunktion.
• Die Punktedichte passt sich automatisch an die Nichtlinearitäten der Übertragungsfunktion an.
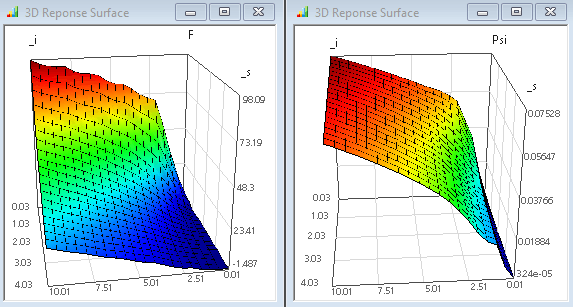
• Mit dem erhaltenen Ergebnis kann man noch experimentieren, indem man das "Adaptive Sampling" deaktiviert und mit verschiedenen Konfigurationen (Covarianz und Polynomordnung) jeweils die Antwortflächen neu berechnet. Bei automatischer ermittlung der "Best Covarianz" ergaben sich z.B. physikalisch durchaus sinnvollere Ersatzfunktionen (geringere negative Kraft, monotoner Psi-Verlauf):

• Für "gutmütige" Übertragungsfunktionen (wie in unserem Magnet-Beispiel) bringt der adaptive Gauß-Prozess meist keine Berechnungs- und Genauigkeitsvorteile im Vergleich zur klassischen Abtastung mittels Rastersuche.
• Eine einmalige, vertrauenswürdige Approximation der Antwortflächen mittels relativ feiner Abtastung bildet die Grundlage, um z.B. mit einer gröberen Abtastung im weiteren Prozess trotzdem hinreichend genaue Ersatzmodelle zu erzeugen.
• Unser Beispiel zeigte, das der "normale" Gauß-Prozess bei einem 6-stufigem Full Factory Design ähnlich genaue Ergebnisse liefern kann:
  
• Nach einer Änderung des FEM-Modell kommt man mit diesem Wissen relativ schnell wieder zu einem hinreichend genauem Ersatzmodell für die Dynamik-Simulation des Magnet-Antriebs.

Komplex 5 der Lehrveranstaltung Finite Elemente Methode endet an dieser Stelle. Hier geht es zurück zur Startseite.

← →