Software: FEM - Tutorial - Magnetfeld - Kraft und Koppelfluss

↑

← →

Kraft und Koppelfluss (Einführung)

Magnetkraft

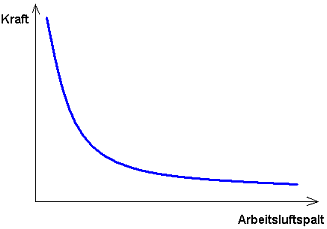
Die im Arbeitsluftspalt s eines Elektromagneten erzeugte Kraft ist abhängig von der Stärke des Spulenstroms i. Aber noch stärker hängt diese Kraft von der Größe des Arbeitsluftspalts ab. Bei konstantem Spulenstrom steigt die Kraft mit kleiner werdendem Luftspalt sehr stark an:

Eine statische FEM-Simulation ergibt bei einem vorgegebenen Spulenstrom nur den Kraftwert für den aktuell eingestellten Arbeitsluftspalt. Interessiert man sich für das Kennfeld F=f(s,i), so kann man dieses nur über eine Abfolge von FEM-Simulationen mit systematisch geänderten Werten für s und i ermitteln:

• Für diese systematische Variation der Parameterwerte s und i werden wir die Rastersuche das OptiY-Programms nutzen. Dieses Programm bietet uns auch die Möglichkeit, das gewonnene Kennfeld als 3D-Diagramm zu visualisieren. Wir können uns im Lua-Script also auf die Berechnung der Magnetkraft beschränken.
• Bevor wir das Lua-Script um die Berechnung der Magnetkraft erweitern, wollen wir das Prinzip der Kraftberechnung auf dem Niveau der grafischen Oberfläche erkunden. Voraussetzung ist die vorherige Abarbeitung unseres bisherigen Lua-Scripts.
• Wir betrachten hier 3 unterschiedliche Methoden für die Ermittlung der Magnetkraft.

Kraft auf Trennflächen

• Eine Abschätzung der Magnetkraft ermöglicht bereits die mittlere Flussdichte im Luftspalt zusammen mit der wirksamen Luftspaltfläche über die Maxwellsche Zugkraft-Formel:

F = A·B² / (2·µ₀)

• Bei einem Luftspalt sAnker = 1 mm ergibt sich mit dem Ankerquerschnitt A = 77,7 mm² und der Flussdichte B ≈ 0,4 T eine Kraft F ≈ 5 N.

Gewichtetes "Stress-Tensor-Volumenintegral"

Im Vergleich zur fehlerträchtigen Berechnung nach obiger Formel, ist die im FEMM-Postprocessor implementierte Methode ein Kinderspiel. Unter der Voraussetzung, dass der Magnet-Anker überall an Luft grenzt, braucht man das zugehörige Geometrie-Objekt des Ankers nur markieren und die resultierenden Kräfte aufintegrieren lassen:

• Die Analysen werden in der geöffneten .ans-Datei vorgenommen.
• Man aktiviert den Areas-Operation-Modus .
• Man wählt die Region des Ankers durch Anklicken mit der linken Maustaste (Anker wird "grün").
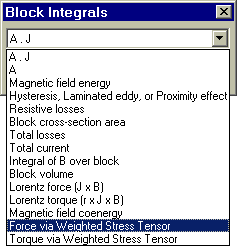
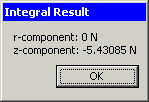
• Nach Aufruf der Integration wählt man die Ermittlung der Kraft mittels "Gewichtetem Stress-Tensor" und erhält sofort das Ergebnis der Integration in einem extra Ausgabefenster:
  
• Der erhaltene Wert ist unter gleichen Bedingungen ca. 10% größer als der vorherige "Schätzwert", der nur die Kraftwirkung im Luftspalt selbst berücksichtigte.
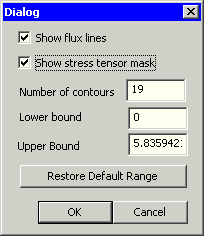
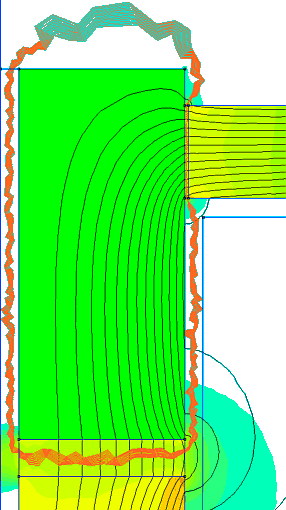
• FEMM legt um die gewählte Region automatisch eine Stress-Tensor-Maske. Diese beschreibt den Weg für die Integration. Um die Maske darzustellen, muss man über den Contour-Plot-Dialog diese Anzeige aktivieren. Die roten Linien repräsentieren die Pfade für die Integration:

• Obiges Ergebnis für die Magnetkraft wurde mit nLuft=3 zur Steuerung der Netzdichte in den Luftspalten ermittelt. Das Gesamtnetz umfasst damit ca. 12500 Knoten und erfordert schon eine merkliche Berechnungszeit.
• Für die systematische Abtastung des Kennfeldes müssen wir sehr viele Modellberechnungen durchführen. Deshalb ist es wichtig, eine hinreichend genaue Kraftberechnung mit einem möglichst groben Netz zu erhalten. Wir testen deshalb im Folgenden für sAnker=1 mm und iSpule=1 A den Einfluss der Vernetzungsfeinheit für nLuft=1..5, indem wir nLuft im Lua-Script manuell ändern und das Script erneut abarbeiten lassen. Dabei schätzen wir auch die Abarbeitungszeit t für das Script. Dafür ergeben sich beispielhaft folgende Werte:

 nLuft | F/N | t/s 
-------------------
  1    |5,30 |  1 
  2    |5,37 |  3 
  3    |5,43 | 12 
  4    |5,44 | 21 
  5    |5,44 | 30 

Man kann aus diesen Ergebnissen zwei wesentliche Erkenntnisse ableiten:

1. Die Kraftberechnung reagiert relativ unempfindlich auf die Vernetzung in den Luftspalten (Fehler max. 2%). Da das Modell auch bei exakter Berechnung infolge der Unbestimmtheit vieler Parameter (insbesondere Material und Restluftspalte) um einige Prozent ungenauer ist, spielt dieser Vernetzungsfehler nur eine untergeordnete Rolle.
2. Die Berechnungszeit für das Modell steigt dramatisch. Man benötigt mindestens die 10-fache Zeit, wenn man Berechnungsungenauigkeiten im Promille-Bereich anstrebt (z.B. nLuft=3). Für die einzelne Modell-Berechnung ist das im Beispiel noch unkritisch. Da für das systematische Abrastern des gewünschten Kennfeldes mindestens 100 bis 400 Modell-Berechnungen erforderlich sind, ist der Unterschied jedoch gewaltig!

Wir setzen deshalb für die weitere Modell-Nutzung im Lua-Script nLuft=1.

Maxwellscher Stress Tensor

Leider ist die soeben beschriebene Methode der Magnetkraft-Bestimmung nicht in allen FEM-Systemen implementiert. Deshalb ist man häufig darauf angewiesen, manuell den Integrationsweg für die Kraftberechnung vorzugeben. Darin liegt jedoch gerade für unerfahrene Nutzer eine nicht zu unterschätzende Fehlerquelle:

• Ursächlich sind numerische Probleme bei der im Hintergrund erforderlichen Ermittlung von B und H mittels numerischer Differentiation aus dem Primärergebnis "Vektorpotential A".
• Besonders falsch werden B und H an der Grenze zwischen Materialien unterschiedlicher Permeabilität berechnet (z.B. Luft / Eisen).

Daraus resultieren folgende Regeln:

1. Der Integrationsweg darf nie direkt an der Grenze zwischen verschiedenen Materialien verlaufen.
2. Es sollten mindestens 2 Elemente zwischen dem Integrationspfad und der Grenze des interessierenden Objekts (hier der Anker) liegen.
3. An den kritischen Stellen rings um das interessierende Objekt sollte man eine möglichst feine Vernetzung verwenden, um "stochastische" Sprünge bei der numerischen Differentiation des Vektorpotentials zu minimieren.

• Wenn man unser Beispiel betrachtet, so sieht man, dass mit der aktuellen Vernetzung obige Regeln nicht befolgt werden können.
• Auf Grund des Aufwandes soll diese allgemeine Methode in dieser Übung nicht praktisch erprobt werden!

Koppelfluss

• Für die Berechnung des Koppelflusses Ψ (auch Verkettungsfluss genannt) werden die magnetischen Flüsse über alle Windungen w aufsummiert. Handelt es sich um eine einlagige Zylinderspule im homogenen Feld, so gilt für diesen Spezialfall Ψ=w·Ф.
• Man benötigt den Koppelfluss Ψ für die Berechnung der in der Spule infolge von Flussänderungen induzierten Spannung v_ind=dΨ/dt.
• Daraus resultiert auch die Bezeichnung Koppelfluss, weil er als integrale Größe die Wechselwirkung (die Kopplung mit dem Magnetfeld) auf der elektrischen Seite des elektro-mechanischen Wandlers repräsentiert.
• Der Wert des Koppelflusses (Flux Linkage) einer Spule wird im magnetischen Postprozessor des FEMM-Programms als Bestandteil der Circuit Properties 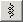berechnet. Der Einfluss der groben Vernetzung mit nLuft=1 beträgt wie bei der Kraftberechnung ca. 2%.

← →