Software: FEM - Tutorial - Magnetfeld - Material und Stromkreis
Material
Es ist sinnvoll, die Geometrie nicht losgelöst von den stofflich-physikalischen Eigenschaften zu beschreiben. Deshalb sollte man vor der Geometrie alle benötigten Modell-Materialien definieren. Als zusätzliche physikalische Eigenschaften sind z.B. in Magnetkreisen die Eigenschaften der Wicklungsstromkreise zu beschreiben.
Die benötigten Materialien (Luft, Kupferdraht, Eisen) müssen innerhalb des Modells als "Model Materials" definiert werden.
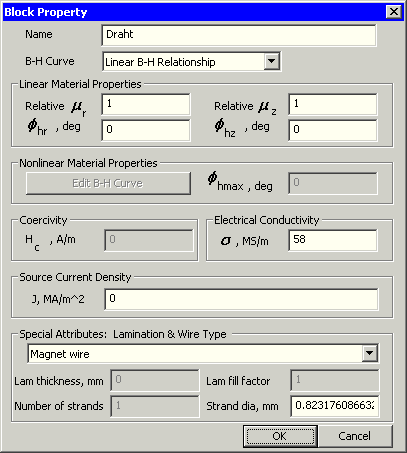
Draht
- Für den Kupfer-Draht wurde die spezifische Leitfähigkeit von 58 MS/m benutzt.
- Zur richtigen Modellierung des Wickelraums ist die benutzte Cu-Drahtstärke anzugeben:
- Dafür gilt näherungsweise: d=√ (h·b)/w - dLack.
- Je nach vorgegebener Windungszahl und Magnet-Geometrie wird eine andere Drahtstärke gewählt. Dabei müsste man eigentlich berücksichtigen, dass nur eine bestimmte Reihe von Drahtdurchmessern verfügbar ist. Aus Aufwandsgründen nutzen wir hier nur obige Näherungsformel!
-------------------------------------------------------------------------------
-- Materialien (Luft, Kupfer, Eisen) --
-------------------------------------------------------------------------------
-- mux, muy : rel. Permeabilitaet in x- bzw. y-Richtung (hier r bzw. z)
-- Hc : Koerzitivfeldstärke [A/m] -> hier Null
-- J : aktuelle Stromdichte [A/mm²] -> hier Null
-- Cduct : spez. Leitfähigkeit [MS/m] -> nur bei Kupferdraht
-- LamD : Schichtdicke [mm] -> falls Laminat-Type<>0
-- PhiHmax : Hysterese-Verlustwinkel [deg] -> genutzt für BH-Kurve
-- LamFill : Material-Fuellgrad des Volumens -> 1=komplett gefüllt
-- LamTyp : Laminierungstype, z.B. 0=massiv oder in Ebene / 3=Magnetspule
-- PhiHx, PhiHy : Hysterese-Verlustwinkel [deg] -> genutzt fuer µ=konst.
-- nStr : Zahl der Einzeldrähte in Spule -> 1 in der Magnetspule
-- dWire : Durchmesser Cu im Spulendraht [mm]
bSpule = 0.5*(dMagnet-dAnker)-dWand-2*sWickel; -- Breite Wickelfenster
hSpule = hTopf-hDeckel-2*sWickel; -- Höhe Wickelfenster
dWire = sqrt(hSpule*bSpule/wSpule)-dLack;
mue = 400; -- nicht mehr wirksam, wenn B-H-Kennlinie definiert!
-- mi_addmaterial(’name’ ,mux,muy,Hc,J,Cduct,LamD,PhiHmax,LamFill,LamTyp,PhiHx,PhiHy,nStr,dWire);
mi_addmaterial("Luft" , 1, 1, 0,0, 0, 0, 0, 1, 0, 0, 0, 0, 0 );
mi_addmaterial("Draht", 1, 1, 0,0, 58, 0, 0, 1, 3, 0, 0, 1,dWire);
mi_addmaterial("Stahl",mue,mue, 0,0, 0, 0, 0, 1, 0, 0, 0, 0, 0 );
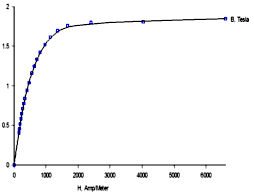
-- B-H-Kennlinie Stahl (Vielzahl der Ziffern aus Umrechnung der µ(B)-Funktion)
mi_addbhpoint("Stahl", 0 , 0 );
mi_addbhpoint("Stahl", 0.2004 , 318.31 );
mi_addbhpoint("Stahl", 0.6008 , 636.62 );
mi_addbhpoint("Stahl", 1.102 , 1591.55 );
mi_addbhpoint("Stahl", 1.386 , 4774.65 );
mi_addbhpoint("Stahl", 1.465 , 7957.75 );
mi_addbhpoint("Stahl", 1.667548, 32902.23251);
mi_addbhpoint("Stahl", 1.789509, 92585.3973 );
mi_addbhpoint("Stahl", 1.878209, 160685.3549 );
mi_addbhpoint("Stahl", 2.08 , 318310 );
Die BH-Kurve muss in FE-Modellen so gestaltet werden, dass die daraus resultierende µ(B)-Funktion monoton fällt. Ansonsten entstehen numerische Probleme mit dem Gleichungslöser infolge von Mehrdeutigkeiten.
Die originale µ(B)-Kurve wird deshalb für kleine Flussdichten nicht nachgebildet, sondern die µ(B)-Kurve beginnt mit einem µ, welches etwas größer als der eigentliche Maximalwert von µ ist!
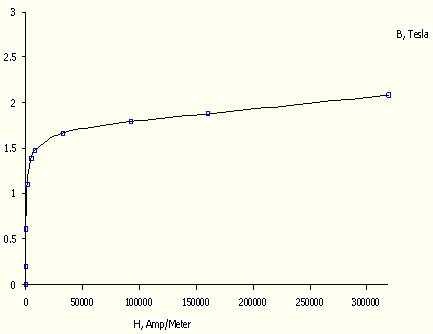
Das FEMM-System benötigt die zugehörige BH-Kennlinie, die in Form von Stützstellen einzugeben ist. Über diese Stützstellen interpoliert der Solver mittels einer Spline-Funktion. Da für die Berechnung der Haltekraft die Sättigung des Eisens bei hohen Flussdichten entscheidend ist, muss viel Sorgfalt auf die Nachbildung des µ-Wertes für hohe Flussdichten aufgewandt werden. Dieser Wert entspricht dem Anstieg der BH-Kennlinie am Ende. Hier muss (wie im Beispiel) meist noch eine "künstliche" Stützstelle für sehr hohe Feldstärken ergänzt werden.
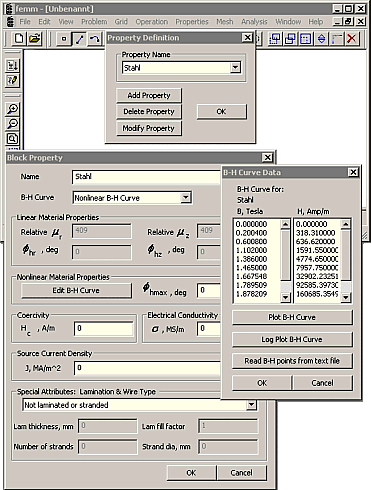
Nachdem im FEMM obige LUA-Script-Anweisungen abgearbeitet wurden, kann man die daraus resultierenden Material-Definitionen überprüfen (Menü-Punkt Properties - Material):
Stahl
- Nach dem Selektieren von Stahl gelangt man über den Button Modify Property zu den Stahl-Parametern.
- Die elektrische Leitfähigkeit des Eisenmaterials wurde Null gesetzt, weil sie für statische Berechnungen keine Rolle spielt (keine Wirbelströme)!
- Der Button Edit B-H-Curve führt zur Liste der Kennlinien-Punkte.
- Mittels Plot B-H-Curve erhält man die Grafik des zugehörigen Funktionsverlaufs:
Luft
Stromkreis
- Der Bereich der Spulenwicklung muss noch näher spezifiziert werden. Es handelt sich um einen elektrischen Kreis mit eingeprägtem Strom.
- Eigenschaften solcher elektrischen Kreise werden im FEMM als "Circuit Property" beschrieben:
-------------------------------------------------------------------------------
-- Circuit Property für die Wicklung definieren (Strom und Wicklungstyp --
-------------------------------------------------------------------------------
-- mi_addcircprop("circuitname", i, type) i: Strom / type: 0=parallel 1=seriell
mi_addcircprop("Spule", iSpule, 1);
- Nach Abarbeitung des LUA-Scripts kann man die erfolgreiche Definition dieses Spulen-Stromkreises auf der grafischen Oberfläche unter Properties - Circuits - Modify Property überprüfen: