Software: FEM - Tutorial - Magnetfeld - Probabilistik - Monte-Carlo

↑

← →

Probabilistische Simulation - Verfahren mit Zufallszahlen (Monte Carlo)

Es existieren verschiedene Verfahren, wie man durch "Würfeln" Verteilungsdichten über die Streubreite der Parameter nachbilden kann. Man spricht hierbei auch von Sampling-Verfahren oder Monte-Carlo-Verfahren. (Siehe "OptiY-Hilfe: Theoretische Grundlagen > Statistische Versuchsplanung > Sampling Verfahren). Wir werden uns hier auf das Rechenzeit-optimale Verfahren des Latin Hypercube Sampling beschränken.

Achtung:
Falls es noch nicht geschehen ist - man muss "Simulation" als Optimierungsverfahren wählen! Damit wird nur eine Stichprobe simuliert.

Versuchsplanung

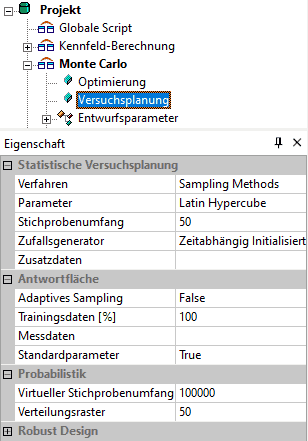
Das Latin Hypercube Sampling ist eine geeignete Sampling-Methode, um in unserem Beispiel mit akzeptablem Berechnungsaufwand hinreichend genaue und anschauliche Ergebnisse zu erhalten. Bei diesem Verfahren wird der gesamte Streubereich jedes Parameters in Intervalle unterteilt. Innerhalb dieser Intervalle werden entsprechend der Verteilungsdichte Werte "erwürfelt":

• Der gewählte Stichprobenumfang von 50 ist ein guter Kompromiss um einen Eindruck von dieser Methode zu erhalten.
• Der Zufallsgenerator soll im Beispiel Zufallszahlen in Abhängigkeit von der aktuellen Computer-Zeit liefern, d.h. bei jedem Experiment werden, wie in der Realität, etwas andere Ergebnisse entstehen!

Die Analyse-Diagramme zur Bewertung der probabilistischen Simulationsergebnisse werden bei den Sampling-Methoden nur teilweise auf Basis der wirklich berechneten Stichprobe generiert:

• Aus den mit dem Stichprobenumfang (im Beispiel =50) "erwürfelten" Werten der streuenden Parametern (hier die Luftspalte) und jeder daraus berechneten Bewertungsgröße des Modells (hier Magnetkraft und Koppelfluss) wird nach der Methode der kleinsten Fehlerquadrate eine Übertragungsfunktion approximiert.
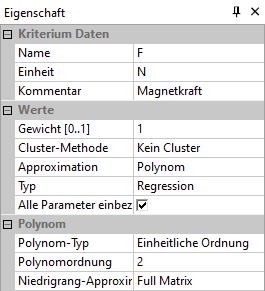
• Für jede Bewertungsgröße (im Beispiel die Gütekriterien F und Psi) kann man unabhängig voneinander eine geeignete Funktion für die Approximation des Übertragungsverhaltens wählen. Wir verwenden hier "Polynom 2. Ordnung" für beide Größen.
• "Einheitliche Ordnung" bedeutet hierbei, dass die angegebene Ordnung für die Abhängigkeit von jeder Streugröße zu verwenden ist:
  
• Eine virtuelle Stichprobe (im Beispiel Stichprobenumfang=100000) wird auf Grundlage der zuvor approximierten Übertragungsfunktionen (= Ersatzmodell für das originale Simulationsmodell) generiert.
• Welche Punkte dieses Ersatzmodells für eine virtuelle Stichprobe benutzt werden, wird gleichfalls mit der für die reale Stichprobe gewählten Sampling-Methode "erwürfelt" (im Beispiel Latin Hypercube).
• Mit virtuellen Stichproben erhält man anschaulichere, "geglättete" Darstellungen auch bei einem kleinen realen Stichprobenumfang. Die Anzahl der Verteilungspunkte entspricht der Anzahl der Intervalle, in welche jeder Streubereich gleichmäßig geteilt wird, um stetige Verteilungsdichtefunktionen aus den diskreten Werten zu ermitteln.

Analyse

Reale Stichprobe

Alle Exemplare der realen Stichprobe werden auf Grundlage des Experiment-Workflows berechnet:

• Jedes Exemplar der Stichprobe ist gekennzeichnet durch seine konkreten Parameter-Werte (Nennwerte und Istwerte der Streugrößen) und die daraus resultierenden konkreten Bewertungsgrößen (Gütekriterien / Restriktionen).
• Bei der Abarbeitung des Workflows werden die in den Workflow eingebundenen Simulationsmodelle berechnet, was sehr zeitaufwändig sein kann.
• Die reale Stichprobe wird nur berechnet nach einem Start des Experiments bzw. dessen Weiter-Führung nach Stopp .

Bei der Nutzung von Sampling-Verfahren kann man bereits während der Simulation den Verlauf des Experiments beobachten:

• Wie in der Realität wird aus der gesamten Stichprobe ein Modell-Exemplar nach dem nächsten untersucht.
• Die generierten Werte der streuenden Parameter und die Ergebnisgrößen (Gütekriterien und Restriktionen) können für jede einzelne Modellrechnung mittels der bereitgestellten Analyse-Funktionen dargestellt werden.
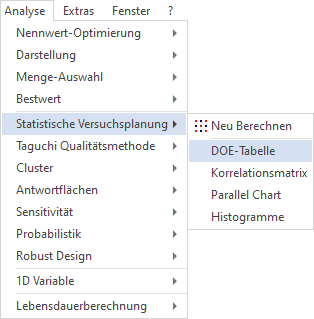
• Die Darstellmöglichkeiten, welche sich nur auf die Ergebnisse der realen Stichprobe beziehen, findet man im Menü Analyse > Statistische Versuchsplanung.
• Wir werden im Folgenden die einzelnen Darstellungen einzeln aktivieren.

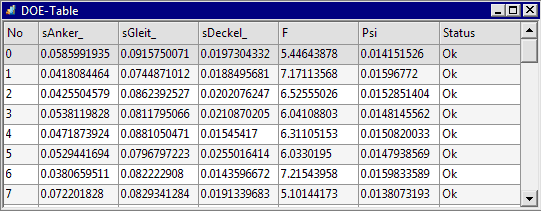
DOE-Tabelle

Wir beginnen mit der DOE-Tabelle. In dieser werden alle Werte der realen Stichproben-Exemplare in der Reihenfolge ihrer Berechnung aufgelistet:

• DOE="Design of Experiments" (Versuchsplanung).
• Listet für jede Modellrechnung der echten Stichprobe (=1 Zeile) in den Spalten eine Auswahl von allen im Workflow definierten Größen auf.
• Über die Menü-Funktion Datei - Daten Export kann man diese umfangreichen Datensätze der DOE-Tabelle bei Bedarf in einer Excel-Datei weiter verarbeiten:
  

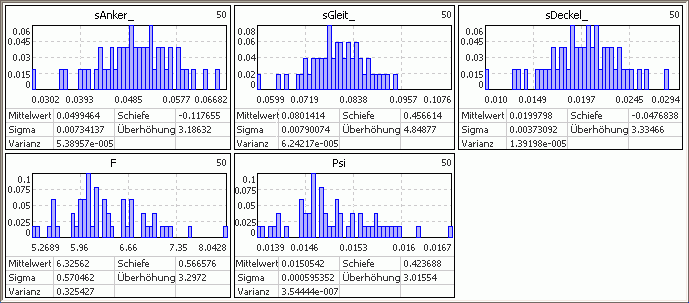
Histogramme

Histogramme stellen die Häufigkeitsverteilung der abgebildeten Größen innerhalb des Streubereiches dar. Die Streugrößen der Luftspalte, die Kraft F und den Koppelfluss Psi ziehen wir mit Drag &  Drop in das anfangs leere Histogramm-Fenster:

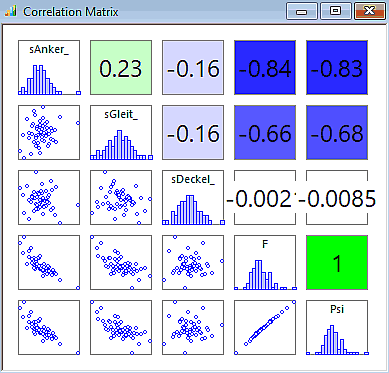
Korrelationsmatrix

Es wird für die reale Stichprobe die Korrelation zwischen allen Parameter-Streuungen und Bewertungsgrößen in Form von linearen Spearman Korrelationskoeffizienten dargestellt. Der Koeffizient K mit einem Bereich von -1 bis +1 ist auch farblich gekennzeichnet:

• |K|=0 → keine Korrelation mit der Toleranzgröße (weiß)
• |K|=1 → starke Korrelation mit der Toleranzgröße (dunkelblau).

Interpretation:

• Entlang der Diagonalen sind die einzelnen Streuungen als Histogramme eingetragen.
• Die 2D-Anthill-Plots unterhalb der Diagonalen stellen den Zusammenhang zwischen jeweils zwei Streuungen dar.
• Welche zwei Streuungen dies jeweils sind, ergibt sich durch Verfolgen der Spalte und Zeile bis zur Diagonalen.
• Spiegelbildlich zu den 2D-Anthill-Plots befinden sich oberhalb die zugehörigen Korrelationskoeffizienten.
• Falls die Bildung der Zufallszahlen gut funktioniert, darf keine Korrelation zwischen unterschiedlichen Parameter-Streuungen existieren (K=0). Auf Grund der kleinen Stichprobe ist ca. K<0.2. Die Korrelation zwischen streuenden Parametern hat insbesondere Bedeutung bei der Benutzung von Messwerten.
• Die Korrelation zwischen streuenden Parametern und Bewertungsgrößen ist abhängig vom Übertragungsverhalten des Modells.
• Achtung: Korrelation bedeutet nicht "kausale Abhängigkeit"! In technischen Anwendungen verbirgt sich dahinter aber meist eine Ursache-Wirkungs-Beziehung.

Anthill-Plot

Der "Ameisenhaufen" stand Pate für die Bezeichnung dieser Darstellform (Punktdiagramm), welche auch als Streudiagramm (engl. Scatterplot) bekannt ist. In OptiY existieren zwei Formen von Anthill-Plots (Analyse > Cluster > Anthill-Plot):

2D-Anthill-Plot:

• Die X- und Y-Achse sind frei belegbar mit den im Workflow definierten Größen.
• Jedes Exemplar der realen Stichprobe wird durch einen Punkt repräsentiert:
  
• Je mehr die Punktwolke in einem dieser Scatter-Plots sich der Form einer Geraden annähert, desto stärker korrelieren die Werte der beiden dargestellten Größen. Im Beispiel korreliert die Magnetkraft F am stärksten mit dem Arbeitsluftspalt sAnker.
• Wenn man innerhalb der DOE-Tabelle eine Zeile mit Doppelklick auswählt (= Exemplar der Stichprobe), so wird der zugehörige Punkt in allen Anthill-Plots hervorgehoben und es werden daneben die "Koordinatenwerte" eingeblendet.

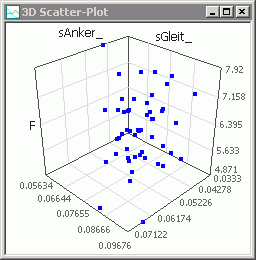
3D-Anthill-Plot:

• Es besteht auch die Möglichkeit, die Abhängigkeit einer Ergebnis-Größe (z.B. der Magnetkraft) von zwei Streu-Größen darzustellen.
• Jedes Exemplar der virtuellen Stichprobe wird ebenfalls durch einen Punkt repräsentiert:
  
• Die X-, Y- und Z-Achsen dieses 3D-Scatter-Plot sind frei belegbar mit den im Workflow definierten Größen.
• Im obigen Beispiel wurde die Kraft als Funktion des Ankerluftspalts und des Führungsspalts dargestellt.

---

Virtuelle Stichprobe

• Für die Simulation einer virtuellen Stichprobe wird das Ersatzmodell genutzt, welches auf Basis der realen Stichprobe gebildet wird. Die Details der Ersatzmodell-Bildung betrachten wir später.
• Der Umfang einer virtuellen Stichprobe kann sehr groß gewählt werden, da die Ersatzmodelle um Größenordnungen schneller rechnen als die Originalmodelle.
• Damit können statistischen Aussagen zu den Ersatzfunktionen praktisch mit beliebiger Genauigkeit gewonnen werden. Die statistischen Ergebnisse zu den Verteilungen und Sensitivitäten können über Analyse > Probabilistik bzw. Analyse > Sensitivität abgerufen werden.
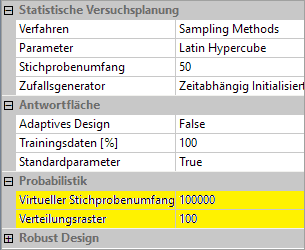
• Die Anzahl der virtuellen Exemplare wird vorgegeben durch den "Virtuellen Stichprobenumfang" in der Konfiguration der Versuchsplanung.
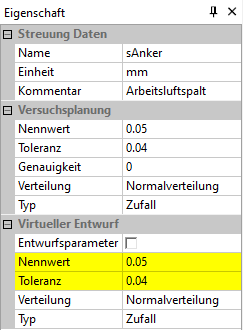
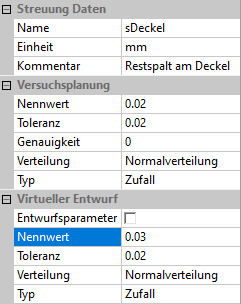
• Der virtuelle Nennwert (=Toleranzmittenwert) und die virtuelle Toleranz können unabhängig vom Toleranzmittenwert und Streubreite der realen Stichprobe gewählt werden. Da uns das Verhalten für die aktuelle Magnetgeometrie interessiert, benutzen wir die gleichen Werte, wie in der realen Stichprobe.
• Mit dem Ersatzmodell kann man auch eine Optimierung der Streugrößen durchführen, dann müsste man Entwurfsparameter=True setzen. Wir untersuchen jedoch nur den Einfluss der Streuung bei konstantem virtuellen Nennwert:
  
  • (virtueller) Nennwert: Ist der aktuelle Toleranzmittenwert, der unabhängig vom Nennwert und dem Toleranzmittenabstand des realen Modells geändert werden kann.
  • (virtuelle) Toleranz: Bestimmt die wirksame Streubreite bei der Berechnung der virtuellen Stichprobe.
• Unabhängig von den Werten der realen Stichprobe kann man mit virtuellen Stichproben die Auswirkungen von Toleranz- und Mittenwert-Änderungen auf das Verhalten analysieren, ohne erneut aufwändige Modellberechnungen durchführen zu müssen.

Wichtig:
Der Streubereich der virtuellen Stichprobe sollte den Streubereich der realen Stichprobe nicht verlassen. Da das Ersatzmodell nur für den Streubereich der realen Stichprobe ermittelt wurde, käme das einer (meist unzulässigen) Extrapolation des Modellverhaltens gleich!

Die Berechnung der virtuellen Stichprobe erfolgt automatisch nach Abschluss der Berechnung der realen Stichprobe oder nach (Analyse > Probabilistik > Neu Berechnen):

Verteilungen

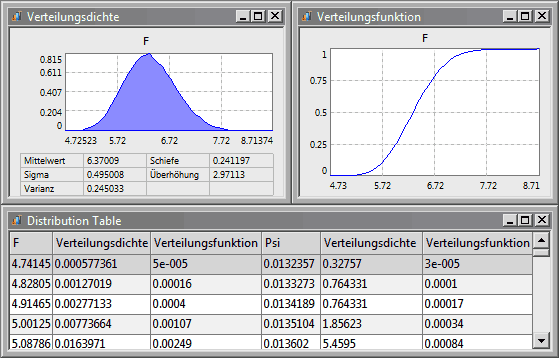
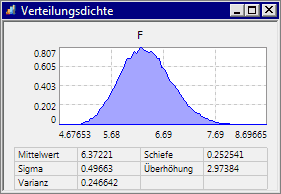
Die Verläufe der Verteilungsdichten und der Verteilungsfunktionen der Ergebnisgrößen werden auf Basis der virtuellen Stichprobe ermittelt. Dabei wird der betrachtete Streu-Bereich der jeweiligen Ergebnisgröße standardmäßig in 50 Stützstellen unterteilt:

Die Verteilungstabelle enthält für alle Ergebnisgrößen die Werte der Verteilungsdichte und -funktion für alle Intervalle entsprechend der Zahl der Verteilungspunkte in der Versuchsplanung. Sie dient vor allem für den Datenexport, um diese Daten mit anderen Programmen weiter verarbeiten zu können.

Der Verlauf der Verteilungsdichte ist im Beispiel etwas unstetig. Dafür gibt es zwei Ursachen:

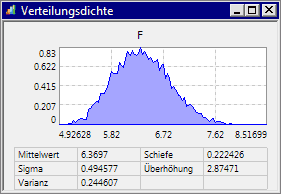
1. Mit steigender Anzahl der Verteilungspunkte (=Intervalle) wird dir Kurve unstetiger. Ändert man im Beispiel die Anzahl auf 100 und berechnet die Probabilistik neu , so ergibt sich der folgende Verlauf:
   
2. Mit steigendem Umfang der virtuellen Stichprobe wird die vom Ersatzmodell bewirkte Verteilungsdichte exakter berechnet. Verringert man den Umfang der virtuellen Stichprobe temporär um den Faktor 10 auf 10000, so ergibt sich mit 100 Intervallen der folgende Verlauf:
   

Sensitivitäten

Sensitivität-Chart:

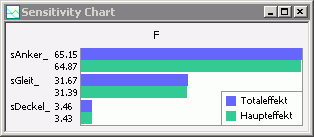
• Es erscheint zuerst ein leeres Fenster, in das man die gewünschten Ausgangsgrößen (Restriktionen bzw. Gütekriterien) per Drag&Drop aus dem Explorer hineinziehen kann. Für jede dieser Ausgangsgrößen wird dann ein Pareto-Chart in Bezug auf alle Streuungen generiert:
• Unter Pareto-Chart versteht man ein Balkendiagramm (Histogramm), das anzeigt, in welchem Maße ein bestimmtes Ergebnis (Effekt) durch eine bestimmte Ursache (Streuung) hervorgerufen wurde. Die Balken sind nach der Größe des Effektes geordnet:
  

Den Pareto-Charts kann man zwei wesentliche Informationen entnehmen:

1. Welche Streu-Größen haben einen vernachlässigbaren Einfluss auf die betrachteten Bewertungsgrößen?
   Im Beispiel hat der Restluftspalt des Deckels nur einen sehr geringen Einfluss auf die Magnetkraft.
   Damit könnte man z.B. für die Optimierung die Streuung dieses Luftspalts unberücksichtigt lassen. Das spart Rechenzeit!
2. Existieren merkliche Interaktionen zwischen den Toleranzgrößen?
   Wenn die aktuellen Ist-Werte der anderen Streuungen den Einfluss der zu betrachtenden Streugröße auf das Verhalten der Bewertungsgrößen merklich verändern, so gibt es Wechselwirkungen zwischen den Streugrößen.
   In den Pareto-Charts erkennt man das an dem Unterschied zwischen den Werten von Total- und Haupteffekt.
   

Existieren (wie im Beispiel) keine merklichen Wechselwirkungen zwischen den Streugrößen, so kann man bei Verwendung der im nächsten Abschnitt beschriebenen Momenten-Methode die probabilistische Simulation mit vereinfachten Ansätzen durchführen. Das spart Rechenzeit!

• Haupteffekt:
  Er repräsentiert den Haupteinfluss der betrachteten Streugröße Xi auf die Ausgangsgröße Y. Definiert ist er als Quotient aus der Varianz der durch Xi verursachten Streuung der Ausgangsgröße Var(Y|Xi) und der Varianz der durch alle Streugrößen X verursachten Streuung Var(Y|X)
  SH = Var(Y|Xi) / Var(Y|X)
• Totaleffekt:
  Er setzt sich zusammen aus dem Haupteffekt und den Interaktionen zwischen den einzelnen Streugrößen (Xi, Xj)
  ST = Var(Y|Xi) / Var(Y|X) + Var(Y|Xi,Xj)/Var(Y|X)

In OptiY wird die Interaktion durch paarweise Kombination aller Streugrößen berücksichtigt, da die gleichzeitige Berücksichtigung sämtlicher Streugrößen zu einem nicht beherrschbaren Berechnungsaufwand führt. Jedes Paar (Xi, Xj) wird als ein Glied dieser Summenformel berücksichtigt. Der Wert dieses Gliedes ist jeweils Null, wenn es keine Interaktion innerhalb des Streugrößen-Paares gibt.

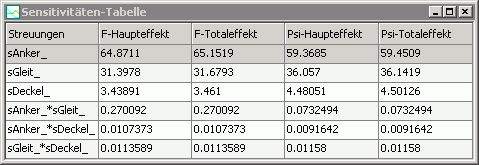
Sensitivität-Tabelle:

• Diese Tabelle zeigt einen kompletten Überblick über die Werte von Haupt- und Totaleffekt der Streuungen auf alle Ergebnisgrößen.
• Über den Kopf der Tabelle kann man die Zeilen nach den unterschiedlichsten Kriterien sortieren:
  
• Zusätzlich zu den Effekten der Streuungen auf die Ausgangsgrößen wird in der Tabelle auch der Effekt der Interaktionen zwischen den Streugrößen auf die Ausgangsgrößen dargestellt.

---

Antwortflächen (Response Surface)

In OptiY finden die probabilistischen Analysen auf Grundlage der approximierten Ersatzmodelle (Übertragungsfunktionen der Ausgangsgrößen) statt. Anhand dieser Übertragungsfunktionen, welche praktisch Flächen im n-Dimensionalen Parameter-Raum darstellen, wird die System-Antwort auf eingespeiste Parameter berechnet. Daraus resultiert die Bezeichnung Response Surface Method (RSM):

Neben verschiedenen Darstellungen dieser Übertragungsfunktionen besteht die Möglichkeit, diese Funktionen z.B. als C-Quelltext zu exportieren. Damit wäre es z.B. möglich, eine Reglerdimensionierung mit einem vereinfachten, schnell rechnenden Ersatzmodell vorzunehmen.

Residuum Plot

• Eigentlich interessieren den Anwender nicht die Aussagen zur Ersatzfunktion, sondern die Eigenschaften des zu untersuchenden Originals. Die Genauigkeit der statistischen Aussagen in Bezug auf das Originalmodell wird überwiegend durch die Genauigkeit der Approximationsfunktionen bestimmt.
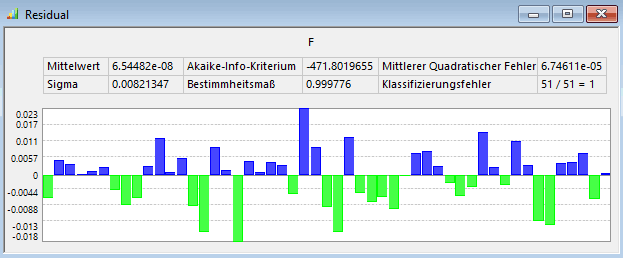
• Die Residuen der Ausgleichsrechnung für eine vorliegende reale Stichprobe zeigen nur, wie genau die Ausgleichsfläche in die vorhandene "Punktwolke" berechneten realen Exemplare passt (Analyse > Antwortflächen > Residuum‑Plot mit Drag&Drop von Kriterium/Restriktion).
• Achtung: Nach einer Überarbeitung der Residuen-Darstellung scheint es ein Problem in der aktuellen OptiY-Version zu geben - vor der Neuberechnung der Ergebnisgrößen erscheinen dann zwar die leeren Diagramme für die darzustellenden Restriktionen/Gütekriterien, aber nach Berechnung der Antwortfläche verschwinden diese wieder und das Fenster ist komplett leer!

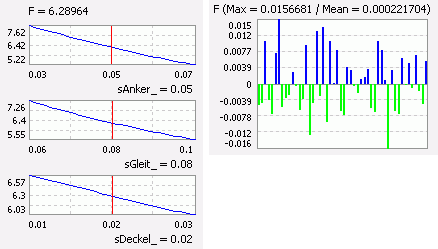
• Residuen sind absolute Differenzen zwischen den "echten" Modellberechnungen und den aus dem Ersatzmodell berechneten Punkten. Im Diagramm kann man den Betrag der maximalen Differenz erkennen. Die Residuen geben damit die Qualität der Approximation an die berechnete Punktwolke wieder. Bei einem Mittelwert der Magnetkraft von 6.3 N sind im Beispiel Abweichungen von max. ca. 0.02 N wahrscheinlich vernachlässigbar!
• Informationen zur Genauigkeit bzw. Sinnfälligkeit der Ausgleichsfläche in den Zwischenräumen der Punktwolke sind damit nicht zu gewinnen.

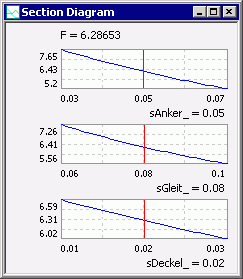
Schnittdiagramm

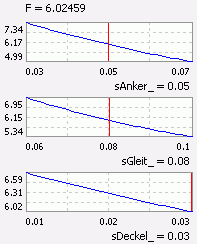
• In einem Schnittdiagramm kann man für die ausgewählten Ergebnisgrößen (im Beispiel die Kraft) den Einfluss ausgewählter Streugrößen (hier der Luftspalte) analysieren.
• Betrachtet man die Abhängigkeit der Magnetkraft F(sAnker_), so gilt die eingezeichnete Kurve nur für die aktuellen Werte aller anderen Streugrößen (roter Strich).
• Ändert man im OptiY-Explorer z.B. den aktuellen Wert des Deckelspalts auf 30 µm, so ändern sich die Kurvenverläufe in den anderen Schnittdiagrammen zu kleineren Kraftwerten:

• 
  Das Kontext-Menü des Schnittdiagramms (Rechtsklick auf ein Schnittdiagramm) bietet zahlreiche Möglichkeiten zur Arbeit mit diesen approximierten Ersatzfunktionen:
  • Damit man nicht den Überblick verliert, welche Istwerte aktuell für alle Streugrößen eingestellt sind, kann man diese z.B. in einer Tabelle als Parameter anzeigen lassen:
    
  • Sinnvoll ist auch das Parameter zurücksetzen auf ihre ursprünglichen Werte.
  • Für die aktuellen Werte kann man eine Simulation durchführen mit dem "echten" Workflow-Modell.

Neu Berechnen

Falls man nicht sicher ist, ob der für die Ergebnisgrößen gewählte Funktionsansatz bzw. die Ordnung der Approximation hinreichend sind, kann man z.B. eine höhere Polynom-Ordnung wählen und die Antwortfläche neu berechnen :

• Dabei wird ohne erneute Modell-Berechnung wieder die echte Stichprobe benutzt.
• Im Beispiel verbessert für die Magnetkraft F eine Erhöhung der Polynom-Ordnung von 2 auf 3 die Anpassung der Ersatzfunktion, was man auch an kleineren Werten im Residuum Plot erkennt:
  
• Nachträglich muss man dann die Neuberechnung der virtuellen Stichprobe veranlassen. Erst danach werden die Verteilungen und Sensitivitäten in den Probabilistik-Diagrammen aktualisiert!

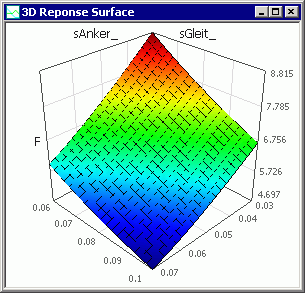
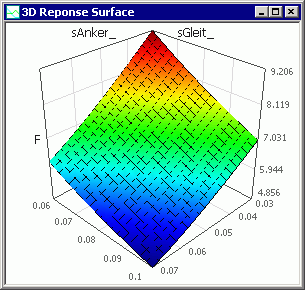
3D-Antwortfläche

• Hier handelt es sich praktisch auch um ein Schnitt-Diagramm. Allerdings wird die ausgewählte Ergebnisgröße hier in Abhängigkeit von 2 Streugrößen dargestellt:
  
• Die dargestellte Übertragungsfunktion ist nur gültig für die aktuellen Werte aller Streu-Größen. Ändert man die aktuellen Werte, so wird die 3D-Antwortfläche aktualisiert. Verringert man z.B. den aktuellen Wert des Luftspalts sDeckel_ von 20 µm auf 10 µm, so entsteht insgesamt eine etwas höhere Magnetkraft:
  

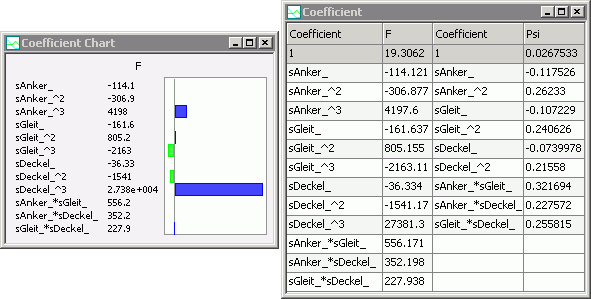
Koeffizienten der Ersatzfunktionen

• Für jede Ergebnisgröße wird eine individuelle Ersatzfunktion approximiert (z.B. Polynom), welche die Abhängigkeit von allen Streugrößen beschreibt. Auf die Koeffizienten jeder dieser Ersatzfunktionen kann man zugreifen (Koeffizient-Chart und Koeffizient-Tabelle). Damit könnte man sich bei Bedarf das approximierte Ersatzmodell in einer anderen Umgebung aufbauen:
  
• Die Koeffizient-Tabelle kann man, wie jede andere Tabelle auch, bei Bedarf z.B. als Excel-Tabelle exportieren (Datei > Daten Export).
• Im Beispiel erkennt man die unterschiedliche Polynom-Ordnung für die Ergebnisgrößen F und Psi.

Modell-Export

Einfacher als mit dem Daten-Export der Koeffizienten-Tabelle erhält man durch Modell-Export sofort einen C-, Modelica-, Visual Basic- oder Matlab-Quelltext des approximierten Ersatzmodells:

• Diese Funktion steht nur in der OptiY Professional Edition zur Verfügung!

Zusammenfassung

Der Vorteil der Sampling-Methode besteht darin, dass mit hinreichend großem Stichprobenumfang beliebige nichtlineare Zusammenhänge zwischen den Streu- und Ergebnisgrößen statistisch erfasst werden können. Von Nachteil ist, dass ein "hinreichend" großer Stichprobenumfang eine sehr große Anzahl vom Exemplaren umfasst (>>1000). Diesen Nachteil kann man durch die Response Surface Methode mildern:

• Im OptiY können z.B. Polynome beliebiger Ordnung als Approximationsfunktion für jede Ergebnisgröße verwendet werden:
  [math]\displaystyle{ P(x) = \sum_{i=0}^n a_ix^i = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_2x^2 + a_1x + a_0 }[/math]
• Durch Anwendung der Methode der kleinsten Fehlerquadrate werden die Parameter der Polynome so bestimmt, dass die Approximationsfunktionen möglichst gut in die Punktwolke der "gesampelten" Stichprobe passen.
• Die minimal erforderliche Anzahl der "echten" Modellberechnungen M (=Stichprobengröße) für die Bildung der Ersatzfunktionen ergibt sich aus der Anzahl n der stochastischen Variablen und der gewählten Ordnung O der Polynom-Funktion zu M=(n²-n)/2+O*n+1.
  Im Beispiel ist M=10 bei n=3 und O=2, was auch mit umfangreichen Modellen noch akzeptable Rechenzeiten ergeben kann.
• Die minimale Stichprobengröße führt jedoch auf Grund der geringen Stützstellendichte nur dann zu einer hinreichend genauen Ersatzfunktion zwischen den Stützstellen, wenn mit dem gewählten Funktionsansatz überhaupt eine sinnvolle Nachbildung des Modellverhaltens möglich ist.
• Die eigentliche statistische Analyse wird mit einer virtuellen Stichprobe sehr großen Umfangs auf Basis des zuvor approximierten Ersatzmodells durchgeführt. Die erreichbare Genauigkeit ist demzufolge nur noch von der Genauigkeit des Ersatzmodelles abhängig!
  ← →