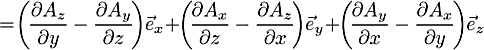Software: FEM - Tutorial - Magnetfeld - Wirbelfeld-Ansatz

↑

← →

Wirbelfeld-Ansatz

Am Beispiel einer 2D-Magnetfeld-Berechnung soll verdeutlicht werden, was sich hinter der Begriffs- und Formelwelt verbirgt, mit welcher man bei der FEM-Simulation konfrontiert wird.

Gewünschte Simulationsergebnisse

In einem abgegrenzten Gebiet der x,y-Ebene sollen die magnetische Induktion B(x,y) und die elektrische Feldstärke E(x,y) als grundlegende Größen berechnet werden:

• Die magnetische Induktion B(x,y) ist ein Vektor in der x,y-Ebene
• Die elektrische Feldstärke E(x,y) ist ein Vektor in z-Richtung (Senkrecht zur Induktion!)
• Alle anderen elektrischen und magnetischen Größen lassen sich über Abhängigkeiten aus B und E berechnen.

Maxwellsche Gleichungen

Der Wirbelfeld-Ansatz berücksichtigt die Verkopplung zwischen dem elektrischen und dem magnetischen Feld über die ersten beiden Maxwellschen Gleichungen sowie die Quelleneigenschaften von magn. und elektrischem Feld:

1. Durchflutungsgesetz (rot H = J + δD / δt)
   Das Umlaufintegral der magn. Feldstärke (MMK) ist gleich der Summe der von diesem Umlauf umfassten Ströme, dies verdeutlicht die Integralform (Gesetz von Stokes).
2. Induktionsgesetz (rot E = -δB / δt)
   Das Umlaufintegral der elektrischen Feldstärke ist gleich der von diesem Umlauf umfassten Flussänderungsgeschwindigkeit (EMK)
3. Quellenfreiheit des Magnetfeldes (div B=0)
   Der in eine Hülle "hineinströmende" Fluss ist gleich dem aus dieser Hülle "herausströmenden" Fluss.
4. Elektrische Ladungsquelle (div D=ρ)
   Die Differenz aus der in eine Hülle hineinströmenden Ladung und der herausströmenden Ladung entspricht der Ladungsänderung des umhüllten Volumens.

Magnetisches Vektorpotential

Das Berechnungsproblem lässt sich numerisch vereinfachen, wenn man es auf die Berechnung des so genannten magnetischen Vektorpotentials reduziert:

• Für beliebige Wirbelfelder (die immer quellenfrei sind!) lässt sich ein "allgemeines" Vektorpotential A definieren (div rot A=0).
• Für magnetische Felder gilt wegen der Quellenfreiheit div B=0.
• Daraus schlussfolgerte Maxwell B=rot A, womit der Zusammenhang zwischen "konkreter" Induktion und "abstraktem" Vektorpotential hergestellt ist.
• Da A als zu berechnende Unbekannte in unserem 2D-Beispiel nur eine Komponente in z-Richtung besitzt, reduziert sich der Rechenaufwand für das Gleichungssystem gewaltig.
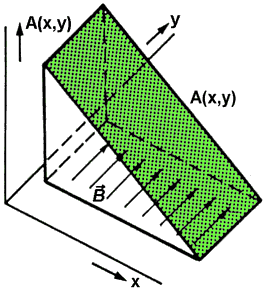
• A(x,y) kann man sich als Lösungsfläche über der betrachteten x,y-Ebene vorstellen, wenn man die Länge z des Vektors A(x,y) als Höhenwert über dem Punkt (x,y) aufträgt.
• Die Neigung dieser Fläche entspricht in jedem Punkt (x,y) der dort vorhandenen Induktion B(x,y):

B_x = δA / δy und B_y = -δA / δx

• Das ergibt sich aus der vollständigen Koordinaten-Darstellung des Differential-Operators rot. Weil A(x,y,z) nur ein Vektor in z-Richtung ist, sind die partiellen Ableitungen von A_x und A_y in alle 3 Koordinatenrichtungen gleich Null:

B(x,y,z) = rot A(x,y,z)

• Das Bild soll den Zusammenhang zwischen dem Vektorpotential A und der Induktion B am Beispiel eines homogenen Magnetfeldes verdeutlichen. Die grüne Fläche repräsentiert das berechnete Vektorpotential. Der negative Anstieg an der Fläche entspricht im Beispiel dem Wert der Induktion in y-Richtung.
• Stellt man das Vektorfeld durch Äquipotentiallinien dar, indem man Punkte gleichen Vektorpotentials (gleicher Höhe) verbindet, so entsteht das Feldlinienbild des Magnetfeldes:
  • Zwischen benachbarten Äquipotentiallinien existieren gleiche Potentialdifferenzen.
  • Starke Anstiege des Vektorfeldes entsprechen großen Induktionswerten und widerspiegeln sich in dicht beieinander liegenden Feldlinien.

← →