Software: FEM - Tutorial - 2D-Bauteil - Ansys - Vergleichsspannung
Aus OptiYummy
Zur Navigation springenZur Suche springen
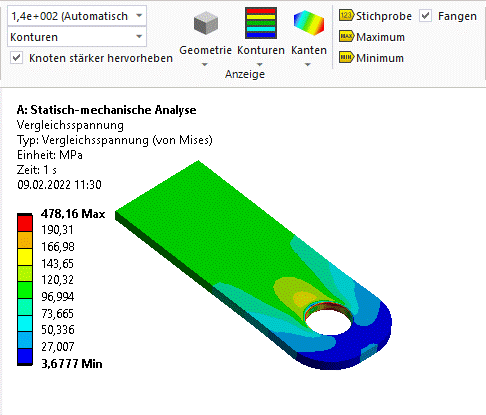
Vergleichsspannung
Es wurde für die Spannungsberechnung die Gestaltänderungsenergiehypothese (GEH) genutzt und damit die sogenannte Mises-Vergleichsspannung ermittelt. Verfügbar sind die berechneten Spannungswerte in allen Elementen. Es gibt verschiedene Möglichkeiten, diese zu ermitteln. Wir betrachten im Folgenden jeweils die Spannung in den Einzelelementen, über Elemente gemittelt und in den sogenannten Gaußpunkten.
- Das entsprechende Ergebnis erhält man wieder über MFL > Ergebnisse > Spannung > Vergleichs- (von Mises)
Legende und Darstellungsoptionen
- Über die MFL sind die bekannten Darstellungsoptionen wählbar (bitte ausprobieren):
- Skalierung der Bauteilverformung: Es sind vorgeschlagene Faktoren oder die Eingabe eines beliebigen Faktors möglich.
- Die Farbkonturen kann man zwischen Isolinien, Konturbändern und "weichen Konturen" umstellen. Letztere vermeiden wir, da sie Unstetigkeiten kaschieren.
- Bei den Modellkanten kann man sich das Netz ein- und ausblenden, sowie Varianten mit Überlagerung durch den unverformten Körper wählen.
- Max- und Min-Werte sowie einzelne Stichproben lassen sich einblenden.
- Die Legende im Grafikbereich ist über das Kontextmenü sehr frei gestaltbar (Ausgangszustand über Rechtsklick > Alles zurücksetzen wiederherstellen):
- Die Grenze der Konturbänder lässt sich per Maus ziehen oder mit einem Klick auf die eingeblendeten Zahlenwerte direkt eingeben.
- Nach Klick auf die Farbleiste kann man mit den angezeigten + und - Symbolen Bereiche hinzufügen oder entfernen.
- Wenn, wie an den Kanten in unserem Beispiel, große Spitzenwerte auftreten, lohnt sich die Option eine logarithmische Skala zu verwenden.
- Die Farben sind frei definierbar. Für Druckerzeugnisse kann die Voreinstellung "Graustufen" hilfreich sein.
Eckknoten-Spannungen
- Die in den Gaußpunkten errechneten Spannungswerte werden zu den Elementknoten hin extrapoliert.
- Ein Eckknoten, der an mehrere Elemente grenzt, erhält also unterschiedliche Spannungswerte von den einzelnen Nachbarn.
- Als Standardeinstellung wird die Knotenspannung zwischen einzelnen Elementen gemittelt. Dadurch ergibt sich ein eindeutiger Wert pro Knoten und stetige Übergänge zwischen den Einzelsegmenten.
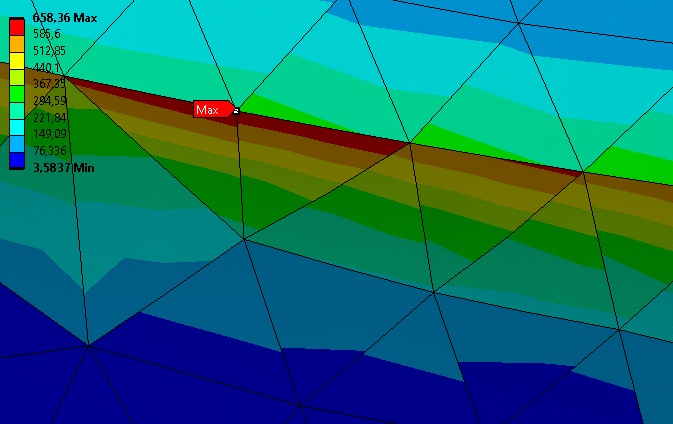
- Wir ändern diese Einstellung in den Details von "Vergleichsspannung" > Integrationspunktergebnisse > Anzeigeoption > nicht gemittelt.
- Sofort fällt auf, dass die Darstellung deutliche Sprünge zwischen den Elementen aufweist.
- Der Spitzenwert von 658 MPa ist deutlich höher als zuvor. Die starken Sprünge im Bereich der Kante zeigen außerdem, dass wieder eine Unstetigkeit auftritt und wir für die hier auftretenden Spannungsgradienten eigentlich zu grob vernetzt haben.
- Bei einer guten Analyse sollte es im Allgemeinen keine starken Sprünge bei der Umstellung auf nicht gemittelte Werte geben. Der konkrete Zahlenwert ist hier deshalb wenig vertrauenswürdig.
Mittlere Element-Spannungen
- Man kann sich die Vergleichsspannung nicht nur für einzelne Knoten, sondern auch gemittelt über das jeweilige Element ausgeben lassen.
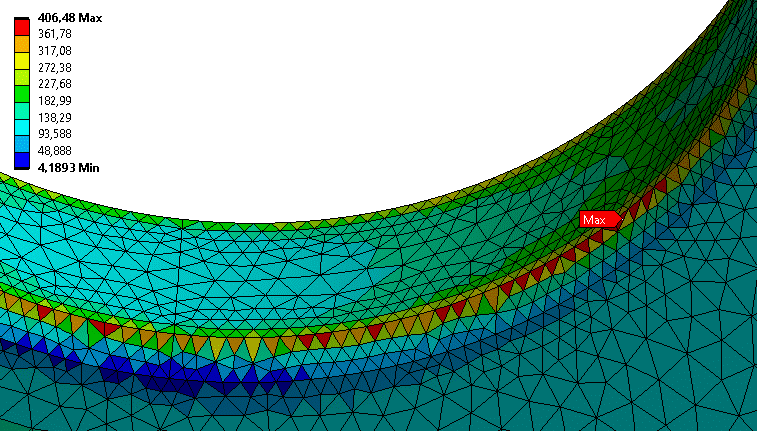
- Dazu die Anzeigeoption auf "Elementbezogener Mittelwert" setzen.
- Jetzt wird der Mittelwert aller enthaltenen Gaußpunkte für das vollständige Element übernommen und jedes Element einheitlich eingefärbt.
- Zwischen Nachbarelementen gibt es dadurch immer noch Sprünge:
- Durch die Mittelwertbildung ist der Maximalwert der Spannung nur noch mit 406 MPa angegeben.
- Daran erkennt man gut, dass der vorherige Spitzenwert extrem stark von seinen direkten Nachbarn abweicht. Im gemittelten Ergebnis "profitieren" die stark belasteten Kanten von ihren schwach belasteten Nachbarn direkt im Lochrand.
Gaußpunkt-Spannungen gemittelt
- Regulär werden die Spannungsergebnisse an den Gaußpunkten zu den Elementknoten hin extrapoliert.
- Man könnte dieses Verhalten über das APDL-Kommando ERESX steuern und direkt die Werte der Gaußpunkte übernehmen, worauf wir aber verzichten.
- Stattdessen betrachten wir hier das "Musterergebnis" mit der Anzeigeoption "gemittelt", welches ohnehin vom Programm vorgeschlagen wurde.
- Die Anzeigeoption wie zu Beginn wieder auf "Gemittelt" stellen:
- Zoomt man die Ansicht größer, erkennt man jetzt gut, dass keine Sprünge mehr zwischen den Elementen vorliegen. Wir wissen aber, dass unser Modell an den Lochkanten Unstetigkeiten aufweist.
- Der Maximalwert der Vergleichsspannung sollte mit etwa 478 MPa niedriger ausfallen als in Fusion 360. Grund dafür ist die geänderte Vernetzung.
- Wir hatten bereits festgestellt, dass die fixierte Konfiguration eine höhere Spannung erreicht, je feiner man das Netz gestaltet.
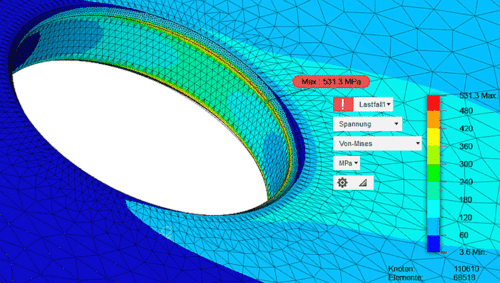
- Ändert man die Vernetzung des Modells so ab, dass an den Kanten ebenfalls die maximale Elementgröße von 0,03 mm erreicht (was wir zu Beginn wegen der Modellgrößen-Beschränkung nicht getan haben), dann erhält man einen Maximalwert von 564 MPa.
- Hinweis: Wer diesen Schritt mit der Studentenversion nachvollziehen möchte, muss die "Elementgröße" auf 0,03 mm reduzieren und nur auf die Lochkante (nicht die Fasenfläche!) anwenden. Außerdem sollte man die adaptive Größe des Netzes wieder aktivieren und den Knotensatz nach dem Vernetzen aktualisiert, da sonst die Kraftrandbedingung nicht mehr funktioniert.
- Dieser Wert stimmt besser überein mit dem Ergebnis entlang der Lochkante aus der Autodesk-Fusion-Studie:
Vernetzungsfeinheit
- Infolge der etwas gröberen Vernetzung des Lochrandes in Ansys weichen die Ergebnisse direkt an der Kante voneinander ab!
- Mit unserem Vorwissen, dass dieser Spannungswert an einer "ideal" eckigen Kante gegen Unendlich läuft, können wir diesen Unterschied erklären.