Software: FEM - Tutorial - 2D-Komponente - Belastung - Modalanalyse

↑

← →

Resonanz-Frequenzen mit fixiertem Lochrand

Unsere Lasche wird nach einer Anregung (z.B. mit einem kurzen Schlag) irgendwie vibrieren. Liegen die Frequenzen der Vibration im Hörbereich, so hört man dies infolge der Luftschall-Übertragung z.B. als "Klirren", was in vielen Situationen als störend empfunden wird.

Mittels der sogenannten Modalfrequenz-Analyse kann man die Eigenfrequenzen (Eigenwerte) und die zugehörigen Eigenschwingungsformen (Eigenformen) ermitteln. Die Modalfrequenz-Analyse (oder kurz Modalanalyse) wird deshalb auch Eigenwertanalyse oder Eigenwertproblem genannt:

• Eigenfrequenz eines schwingfähigen Systems ist eine Frequenz, mit der das System nach einmaliger Anregung schwingen kann.
• Eigenform (auch "Schwingungsmode" oder kurz "Mode") bezeichnet die Form der Schwingung bei einer bestimmten Eigenfrequenz. Unsere fest eingespannte Biegefeder ("verschweißt") wird z.B. vertikal, horizontal oder drehend jeweils mit einer anderen Frequenz in Resonanz schwingen. Zusätzlich gibt es dann für jede diese Schwingungsformen noch die Oberwellen.

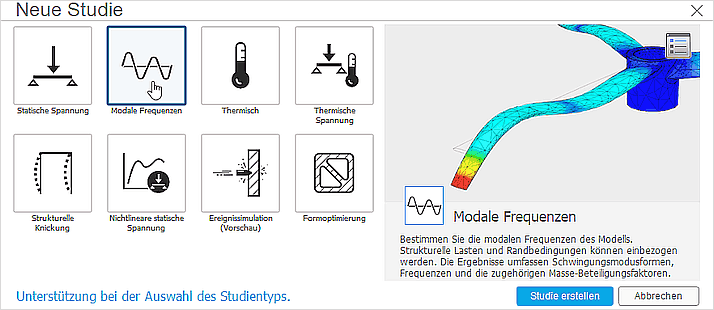
Um Simulationen der Eigenfrequenzen für unsere Lasche im Fusion 360 durchführen zu können, muss man im Arbeitsbereich Simulation eine neue "Studie" erstellen:

• ERGEBNISSE > Ergebnisse fertig stellen führt zurück zur Werkzeugleiste für das EINRICHTEN von Studien.
• EINRICHTEN > Studie > Neue Simulationsstudie bietet nun die Möglichkeit eine Studie für eine Analyse der modaler Frequenzen zu erstellen:
  

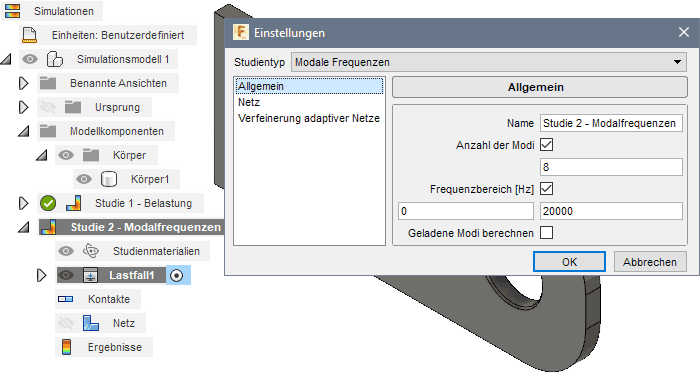
Alle zu einem Simulationsmodell definierten Studien beziehen sich auf die gleichen Körper des CAD-Modells und verwenden standardmäßig das Material aus der Konstruktionsumgebung als Studienmaterial. Die anderen Einstellungen für eine Studie sind individuell vorzunehmen (z.B. mittels Einrichten > Verwalten > Einstellungen):

Uns interessieren im Beispiel nur die prinzipiell vom Menschen hörbaren Eigenfrequenzen bis 20 kHz:

• "Anzahl der Modi" (Eigenfrequenzen), die maximal innerhalb des gewünschten Frequenzbereiches ermittelt werden, ist standardmäßig 8. Die genaue Anzahl kennen wir noch nicht und müssten diese bei Bedarf noch erhöhen.
• "Geladene Modi berechnen" bedeutet, dass vor der Modalanalyse anhand der vorhandenen Lastfälle der Spannungszustand berechnet wird. Dies ist für unseren unbelasteten Zustand nicht erforderlich.

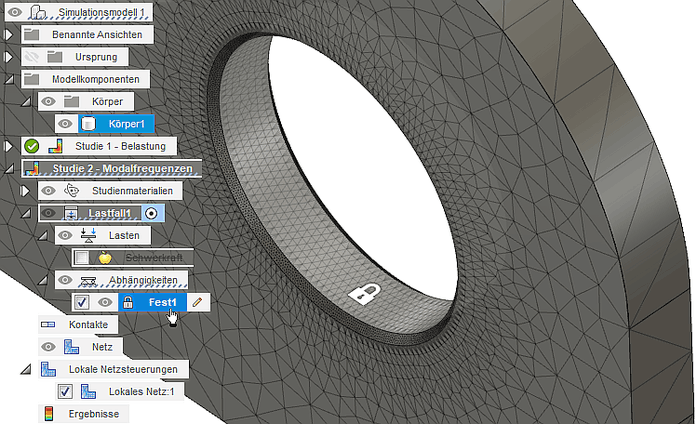
Bei der Vernetzung und Einspannung orientieren wir uns an der Konfiguration der Studie 1 "Belastung" (bzw. Studie 1 "Fest" je nach konkreter Benennung):

• Die feste "Verschweißung" der Lochwand bilden wir durch eine strukturelle Abhängigkeit "Fest" mit der Fixierung aller Freiheitsgrade nach.
• Globale Vernetzung mit einer Elementschicht, lokal eine möglichst feine Vernetzung der beiden Fasen-Flächen.

Ergebnis-Anzeige und -Interpretation

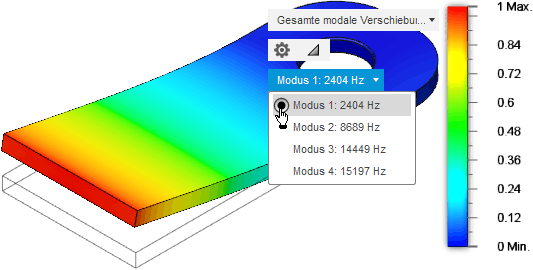
• Nach erfolgreichem Abschluss der Berechnung erfolgt automatisch die Anzeige der Ergebnisse in Form der Visualisierung des Schwingungsmodus für eine gewählte Eigenfrequenz.
• Im Bereich von 0 Hz bis 20 kHz sollten maximal die ersten 8 Eigenfrequenzen beginnend mit der Resonanzfrequenz der tiefsten Grundschwingung berechnet werden:
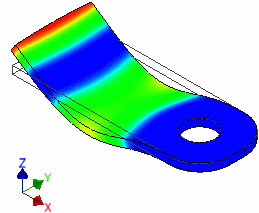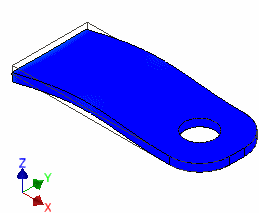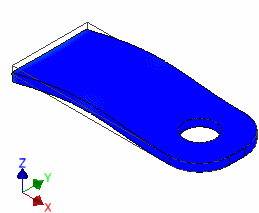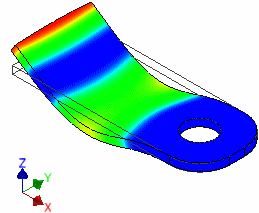
  • Aus der Dropdown-Liste kann man einen Modus für die grafische Visualisierung der Schwingungsform aktivieren (im Bild der Modus 1 bei einer Frequenz von ca. 2,4 kHz):
    
  • Betrachtet man nacheinander die einzelnen Schwingungsmodi, so findet man dabei zusätzlich auch solche mit seitlicher oder rotatorischer Auslenkung als weitere Grundschwingungsformen. Zu diesen gibt es jeweils wieder Formen mit Oberwellen, welche im Beispiel dann aber oberhalb von 20 kHz liegen.

Wichtig:

1. Über reale Amplituden der Schwingungen kann die Modalanalyse keine Aussagen machen. Die angegebenen Werte dienen nur zur Orientierung, wie einzelne Bereiche des Bauteils relativ zu anderen Bereichen ausgelenkt werden.
2. Die Modal-Analyse berücksichtigt nicht die Dämpfung im Material und durch die Randbedingungen. In der Praxis treten deshalb höhere Schwingungsmodi infolge der Dämpfung meist nicht in Erscheinung (Dämpfungskräfte sind proportional zu Relativgeschwindigkeiten, welche sich mit steigender Frequenz ebenfalls erhöhen!).
3. Praktische Bedeutung besitzt deshalb häufig nur die kleinste Eigenfrequenz (Modus 1). Untersuchen sollte man auf Praxisrelevanz jedoch auch die Grundschwingungen höherer Frequenz (prägnant im Beispiel: Rotationsschwinger = Modus 2 / Querschwinger = Modus 4).

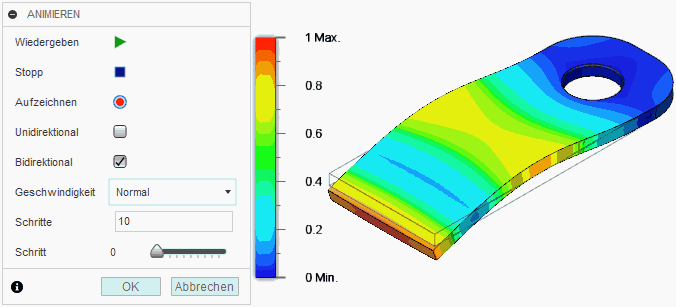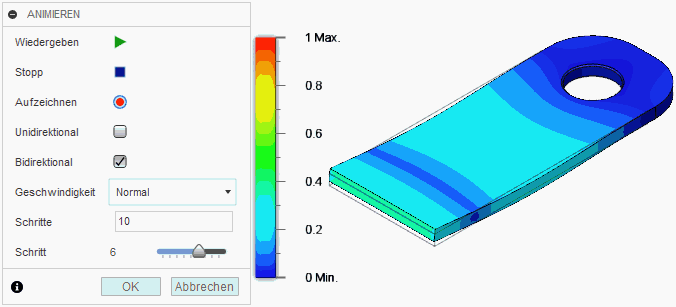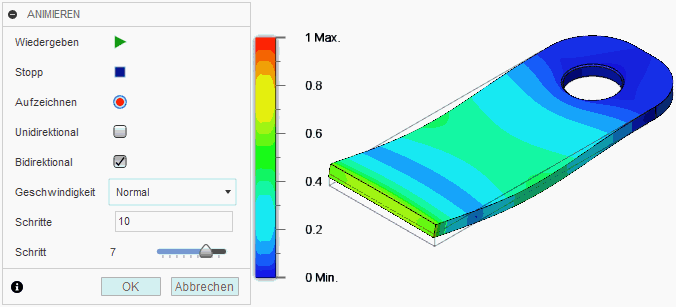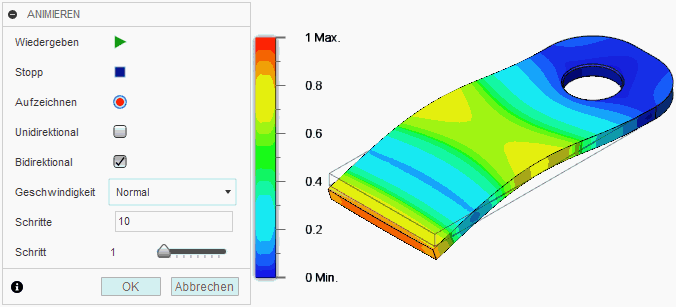
Ergebnisswerkzeuge > Animieren verdeutlicht sehr anschaulich die Eigenform (im Beispiel für Modus 3):

Fragen zur Modalanalyse:

• Welchen Wert besitzt die Resonanzfrequenz der unbelasteten Lasche bei idealisierter starrer Befestigung am Bolzen?
• Wie ändert sich diese Resonanzfrequenz beim Anlegen der maximal zulässigen Zugbelastung aus der Belastungsstudie der "verschweißten" Lasche?
• Die Studie zur Modalanalyse ist mit dieser Zugbelastung als Bestandteil der Lösung einzusenden.

← →