Software: FEM - Tutorial - Magnetfeld - C-Kennfeld Differentierbarkeit

↑

← →

Differenzierbarkeit von Antwortflächen

(Kein Bestandteil der Lehrveranstaltung FEM )

Die Hinweise zur Wahl der Polynomordnung und einer geeigneten Covarianz-Funktion führen in der Systemsimulation nur dann zu nutzbaren Ersatzmodellen, wenn keine numerischen Ableitungen von den identifizierten Kennfeldern benötigt werden:

• Die Differenzierbarkeit der Funktion F(i,s) ist in diesem Sinne unkritisch. Die Beschleunigung a~F stellt die physikalische Größe mit der höchsten Ableitung in der mechanischen Domäne dar. Alle anderen mechanischen Größen ergeben sich durch numerische Integration, welche eventuelle Knicke und Welligkeiten des Kraft-Kennfeldes glättet.
• Dies trifft für den Koppelfluss Psi(i,s) leider nicht zu. Knicke und Welligkeiten dieses Kennfeldes führen zu undefinierten Sprüngen und Richtungsänderungen der an der Spule berechneten induzierten Spannung u_ind=dPsi/dt. Eine Bewertung der Differenzierbarkeit der Antwortflächen im OptiY ist (zurzeit) nur visuell und damit nur sehr eingeschränkt möglich. Es soll deshalb im Folgenden gezeigt werden, wie man das Kennfeld-Testmodell um solch eine Bewertung mit geringem Aufwand ergänzen kann.

Die Differenzierbarkeit einer Funktion mit mehreren Variablen wird am besten durch die Bildung des totalen Differentials erfasst:

• Im Beispiel benötigen wir in der Systemsimulation nur die zeitliche Ableitung dPsi/dt.
• In unserem Testmodell durchlaufen wir für einen vorgegebenen Luftspalt s den Strombereich, indem wir i=t setzen (t=0..10 s).
• Die numerische zeitliche Ableitung u_ind = der(Psi) entspricht demzufolge im Testmodell der partiellen Ableitung dPsi/di.
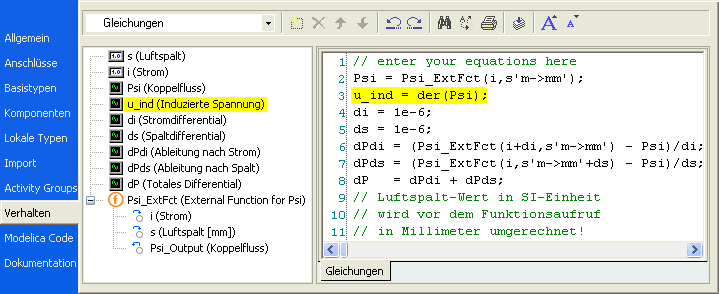
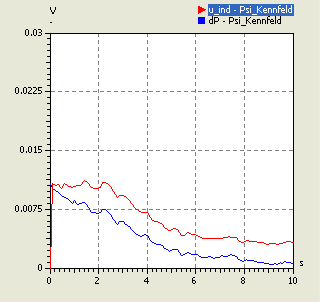
• Es ist zwar relativ einfach, durch Benutzung von Differenzenquotienten die vorhandene Kennfeld-Funktion abzutasten und daraus das totale Differential zu bilden. Im Rahmen der Übung begnügen wir uns jedoch aus Aufwandsgründen mit der Berechnung von u_ind als zeitliche Ableitung von Psi (im Bild des Type-Designers farblich markiert):

• Die Berechnung des totalen Differentials wurde für Interessenten mit dargestellt. Außerdem sollte damit hier im Vergleich gezeigt werden, dass im Beispiel die zeitliche Ableitung bereits die gewünschten Informationen liefert:
  
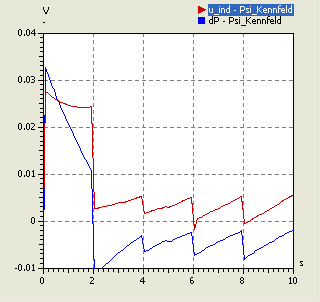
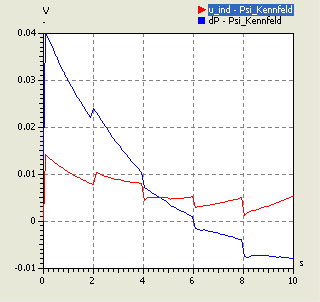
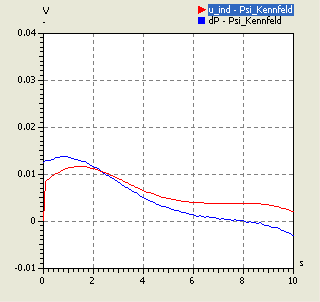
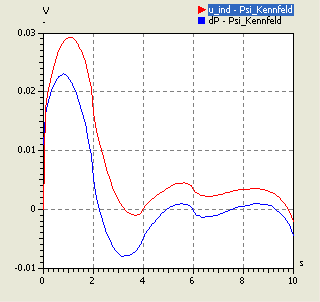
• Die Diagramme (links s=30 µm / rechts s=4 mm) zeigen für die Polynomordnung=0 und Covarianz-Funktion Exponential starke Sprünge. Diese entstehen infolge der Kennfeld-Knicke an den Stützstellen.
• Teilweise können dadurch auch negative Werte für die induzierte Spannung resultieren.
• Die mangelnde Qualität dieser Kennfeld-Funktion widerspiegelt sich in der vereinfachten zeitlichen Ableitung ähnlich wie im totalen Differential.
• Im Beispiel wurde mit dieser Kennfeldfunktion physikalischer Unsinn in einem SimulationX-Magnetmodell berechnet bzw. der Solver verweigerte den Dienst!

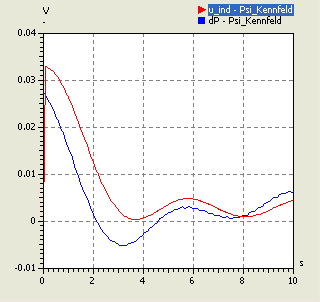
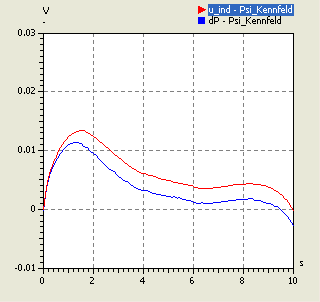
Belässt man die Polynomordnung=0 und ändert die Covarianz-Funktion z.B. zu Square Exponential, so erhält man stetige Ableitungen:

• Jedoch könnten die Welligkeiten insbesondere bei kleineren Luftspalten noch zu negativen Induktionsspannungen führen.
• Die Frequenz der Welligkeit wird durch die Abstände zwischen den berechneten Stützstellen bestimmt und ist physikalisch nicht korrekt.
• Mittels "Durchprobieren" der unterschiedlichen Covarianz-Funktionen kann man versuchen, eine Variante mit minimaler Welligkeit zu finden.
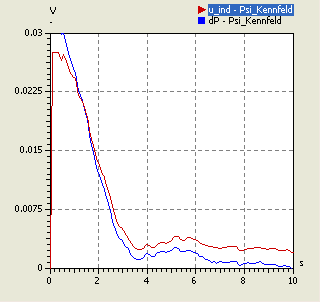
• Ein Psi-Kennfeld ähnlicher Qualität liefert z.B. auch die Covarianz-Funktion Gamma Exponential mit der Polynomordnung=0:
  

Welche Covarianz-Funktion im Zusammenspiel mit welcher Polynomordnung ein Optimum darstellt, muss individuell für jede zu identifizierende Antwortfläche erprobt werden:

• Im Beispiel erwiesen sich nach vielen Versuchen folgende Kombinationen als günstig:

1. F-Kennfeld: Polynomordnung=2 / Covarianz=Exponential
2. Psi-Kennfeld: Polynomordnung=2 / Covarianz=Gamma Exponential

• Die Anwendung des adaptiven Gauss-Prozesses ist meist erforderlich, weil ein gleichmäßiges Grundraster die kritischen Stellen mit großer Wahrscheinlichkeit nicht hinreichend dicht abtastet.
• Durch automatisches Hinzufügen weiterer Abtastpunkte (Berechnungen des FE-Modells), gelang es die folgende Psi-Kennfeldgüte zu erreichen:
  

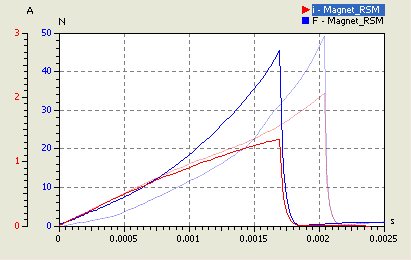
Die Auswirkung der unterschiedlichen Psi-Kennfelder auf das Verhalten eines dynamischen Magnetmodells wird im folgenden Bild durch die Anwendung zweier Kennfelder demonstriert:

• Der eingefrorene (blasse) Signalverlauf wurde mit dem Kennfeld des adaptiven Gauss-Prozesses simuliert.
• Darüber liegt das Verhalten, welches aus dem einfachen Gauss-Prozess mit Covarianz-Funktion Square Exponential resultiert:
  
• Die Ergebnisse unterscheiden sich in Hinblick auf das Zeitverhalten um ca. 20%, was nicht vernachlässigbar ist!

Schlussfolgerung:

• Es ist praktisch nicht möglich, von einer mittels Gaussprozess gebildeten Ersatzfunktion hinreichend genau die partielle Ableitung nach einem der Funktionsparameter zu bilden. Aufgrund von Knicken und Welligkeiten in der Ersatzfunktion entstehen Sprünge und falsche Tendenzen in den Ableitungen.
• Eine praktikable Lösung ist die Bildung des totalen Differentials (z.B. von Psi) direkt im bei der Abtastung des Modells durch Bildung der Differenzenquotienten (im Beispiel dPsi/di und dPsi/ds).
• In der Systemsimulation gewinnt man dann aus dem totalen Differential die benötigte zeitliche Ableitung zurück.

← →