Software: CAD - Tutorial - Kinematik - Einfuehrung
Mit den bisher benutzten Abhängigkeiten ![]() zwischen den Komponenten einer Baugruppe wurden die Freiheitsgrade der Relativbewegung zwischen den Komponenten im Sinne des Zusammenbauens eingeschränkt. Deshalb auch die Bezeichnung "Baugruppen-Abhängigkeit". Ziel war dabei eine eindeutige Position aller Baugruppen-Komponenten zueinander:
zwischen den Komponenten einer Baugruppe wurden die Freiheitsgrade der Relativbewegung zwischen den Komponenten im Sinne des Zusammenbauens eingeschränkt. Deshalb auch die Bezeichnung "Baugruppen-Abhängigkeit". Ziel war dabei eine eindeutige Position aller Baugruppen-Komponenten zueinander:
- Jede Komponente in einer Baugruppe hat unmittelbar nach ihrem Platzieren sechs Freiheitsgrade in Hinblick auf ein Bezugskoordinatensystem:
- Sie ist entlang der X-, der Y- und der Z-Achse verschiebbar (Freiheitsgrade der Translation) und
- um die X-, die Y- und die Z-Achse drehbar (Freiheitsgrade der Drehung).
- Wenn man eine Baugruppen-Abhängigkeit zwischen zwei geometrischen Objekten platziert, entfernt man einen oder mehrere Freiheitsgrade. Das Verschieben bzw. Drehen in die nicht bestimmten Richtungen ist weiterhin möglich.
- Wenn eine Komponente in einer Baugruppe voll bestimmt ist, kann sie sich in keiner Richtung bewegen. Ihre Position ist relativ zu anderen Baugruppenkomponenten festgelegt. Alle Freiheitsgrade sind entfernt.
Alle Freiheitsgrade von Komponenten (Bauteilen bzw. Unterbaugruppen), die in der realen Baugruppe noch existieren, sollten auch im CAD-Modell nicht entfernt werden, z.B.:
- Drehbarkeit von Getrieberädern, Bolzen, Wellen, ...
- Verschiebbarkeit von Getriebegliedern
In einer Getriebe-Baugruppe besitzen die einzelnen Komponenten noch offene Freiheitsgrade für die Bewegung (z.B. noch drehbar oder verschiebbar). Jedoch können sich die einzelnen Komponenten in der Realität häufig nicht unabhängig voneinander bewegen. Die Zwangsbedingungen für die Bewegung zwischen den Komponenten muss man zum Teil mit zusätzlichen Abhängigkeiten beschreiben:
- Im Prinzip kann man Getriebe unter Verwendung der ursprünglichen Zusammenbau-Abhängigkeiten beschreiben, welche wir bisher in der CAD-Übung benutzten.
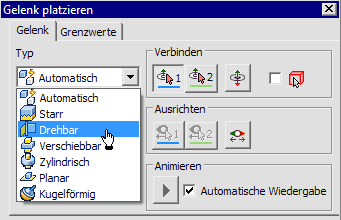
- Günstiger sind die sogenannten (Gelenk-)Verbindungen
 zur Definition von Getriebe-Baugruppen:
zur Definition von Getriebe-Baugruppen: - Vorteile:
- Es sind weniger Beziehungen zwischen den Getriebe-Komponenten erforderlich, als bei Verwendung "primitiver" Baugruppen-Abhängigkeiten.
- Es vereinfacht sich die Aufbereitung des CAD-Modells für die Simulation der Bewegungsabläufe in der Getriebe-Baugruppe.
In dieser Übung üben wir deshalb die Verwendung von Gelenk-Verbindungen als sinnvolle Alternative zu den Baugruppen-Abhängigkeiten, um die realen Gelenke eines Getriebes nachzubilden.
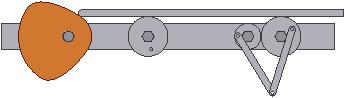
Im ersten Teil des Übungskomplexes soll dafür in Form einer Prinziplösung eine Getriebe-Baugruppe einschließlich ihrer Kinematik modelliert werden:
- Eine translatorische Bewegung (Schub) wird über Reibräder in eine rotatorische Bewegung gewandelt.
- Eines dieser Reibräder treibt ein kleineres Reibrad.
- Die beiden gekoppelten Reibräder treiben einen Mechanismus aus zwei Koppelgliedern.
- Die Schub-Bewegung wird mittels einer Kurvenscheibe erzeugt.
Achtung:
- Hier entsteht nur eine Prinziplösung, mit der die Modellierung der Kinematik demonstriert wird.
- Das Beispielgetriebe wird nur "schematisch" modelliert, Führungen bzw. Andruckfedern werden z.B. vernachlässigt.
- Über Sinn bzw. Unsinn der verwendeten Teile und ihres Zusammenbaus sollte man sich also nicht streiten!