Software: FEM - Tutorial - 2D-Komponente - Belastung - Vergleichsspannung
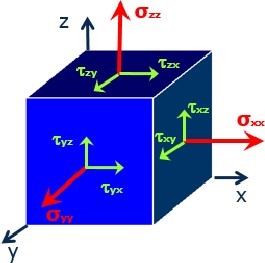
Für das Bauteil wird der dreidimensionale Spannungszustand berechnet. Der Spannungszustand an einer beliebigen Position ist definiert durch:
- drei Normalspannungen (Spannung XX, Spannung YY und Spannung ZZ) sowie
- drei Schubspannungen (Spannung XY, Spannung YZ und Spannung XZ)
Daraus abgeleitet ergeben sich die drei Hauptspannungen, von denen nur zwei praktisch relevant sind:
- 1. Hauptspannung:
repräsentiert die Druckspannung in jedem Punkt - 3. Hauptspannung
repräsentiert die Zugspannung in jedem Punkt
Mittels sogenannter Vergleichsspannungshypothesen werden die Schubspannungen des mehrachsigen Spannungszustandes in äquivalente Normalspannungen umgerechnet, weil die Werkstoffkennwerte nur für den einachsigen Spannungszustand gelten. Dafür gibt es je nach Belastungsfall und Werkstoffeigenschaften unterschiedliche Hypothesen:
- Die Gestaltänderungshypothese (GEH) berechnet die Von-Mises-Spannung, welche für zähe, verformbare Werkstoffe (wie Aluminium, Bronze, Stahl) bei statischer oder wechselnder Belastung als Vergleichsspannungsgröße verwendbar ist. Nur diese Hypothese ist im Fusion implementiert.
- Der Vergleich dieser "Von-Mises-Spannung" mit der Streckgrenze ist eine gängige Methode, um einen Sicherheitsfaktor zu berechnen und das Versagen von verformbaren Materialien vorherzusagen. In der vorliegenden Implementierung basiert die Berechnung auf der Bruchhypothese der maximalen Vergleichsspannung für dehnbare Materialien (von-Mises-Hencky-Theorie).
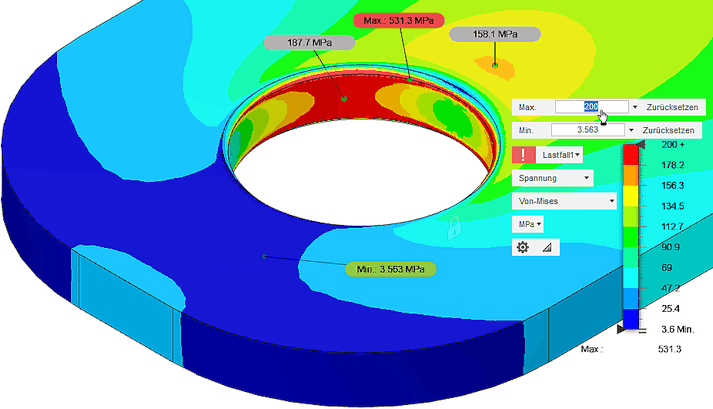
Nach der Simulation haben wir bereits die berechnete mechanische Mises-Vergleichsspannung farblich codiert auf der Oberfläche des Bauteils als "Kontur-Darstellung" angezeigt. Die Farbskala ist dabei automatisch zwischen dem Minimal- und Maximal-Wert der Spannung linear skaliert.
Hinweis:
Die Grenzen der Farbleiste schränken wir auf einen sinnvollen Bereich ein. Die automatische Skalierung "verbrauchte" bereits ca. die Hälfte des Farbspektrums für den engen Bereich am Lochrand:
- Prüfen > Min./Max. einblenden zeigt die Maximalspannung von über 500 MPa auf einer Fasen-Kante direkt an der festen Einspannung. Die konkrete Position des Maximums auf der Kante wird durch numerisches Rauschen bestimmt!
- Ergebniswerkzeuge > Legende Min/Max blendet oberhalb der Farb-Legende Eingabefelder für die Legenden-Grenzwerte ein. Standardmäßig sind diese mit den aktuellen Extremwerten der dargestellten Größe belegt, auf welche jederzeit ein "Zurücksetzen" erfolgen kann. Im Beispiel genügt eine ungefähre Halbierung des Maximalwertes:
- Prüfen > Oberflächenantasten erstellen ermöglicht die Anzeige von Werten für ausgewählte Punkte der Oberfläche. Beispielhaft wurden die Werte für das lokale Maximum unweit des Lochrandes und für das Mitte des stark belasteten Bereiches auf der seitlichen Lochwand eingeblendet. Man sollte damit auch wertmäßig bekannte Spannungswerte überprüfen (Spannung in der Nähe der Last-Zugkraft muss entsprechend der Querschnittsfläche 100 MPa betragen!).
Bewertung der berechneten Maximalspannungen am Lochrand:
- Eventuelle Effekte unrealistisch "scharfer" Kanten wurden durch die Fasen am Lochrand bereits vermieden.
- Die wesentliche Vereinfachung des FEM-Modell besteht noch in der vollständigen Fixierung der Lochwandung. Die Verwendung eines realen Bolzens mit einem E-Modul in der Größenordnung des Materials der Lasche wird zu einem anderen Ergebnis führen!
- Die entscheidende Frage ist nach der Größe des daraus resultierenden Fehlers!
- Mit einer einfachen Überschlagsrechnung kann man zumindest einen Minimalwert der für das statische Gleichgewicht erforderlichen Spannung am Lochrand berechnen. Dabei wird angenommen, dass die Last nur auf der Zugkraft-zugewandten Loch-Seite getragen wird, wie man auch anhand der Spannungsverläufe erkennt:
- Für den homogenen Spannungsverlauf gilt in der Lasche 1000 N/10 mm²=100 MPa (Spannung=Kraft/Querschnitt)
- Der in Kraftrichtung projizierte Querschnitt der angefasten Bohrung beträgt 4 x 0,8 mm²=3,2 mm² → das ergäbe bei homogener Belastung entlang der projizierten Lochwand eine minimal erforderliche Spannung von 312,5 MPa. Da die Belastung insbesondere infolge der Kerbeffekte nicht homogen ist, liegt der berechnete Maximalwert von über 500 MPa entgegen aller vorheriger Überlegungen doch in einem physikalisch glaubwürdigen Bereich!
Wichtig: Die berechneten Ergebnisse sollte man erst nach intensiven Überlegungen akzeptieren!