Software: FEM - Tutorial - 3D-Mechanik - Ansys - Belastungsanalyse Lastfaelle
Flächenlast
Die Konfiguration und insbesondere die Ergebnisse des Projekts zur Simulation einer Streckenlast sollen durch die Analyse weiterer Lastfälle nicht überschrieben werden:
- Deshalb duplizieren wir die bisherige Analyse (Statisch-mechanisch (A5)) über das Kontextmenü.
- Für die beiden Studien vergeben wir sinnvolle Namen: Streckenlast und Flaechenlast
Das Modell soll so konfiguriert werden, als würde die untere Stahlscheibe komplett auf einer Unterlage aufliegen, während auf die obere Scheibe gleichmäßig verteilt eine Kraft von 100 N wirkt:
- Dazu muss die Fixierung der unteren Stahlscheibe umdefiniert werden.
- Auch die "Streckenlast" an der Lochkante der oberen Stahlscheibe ist zu ersetzen durch eine "Flächenlast" auf die Oberseite der oberen Scheibe:
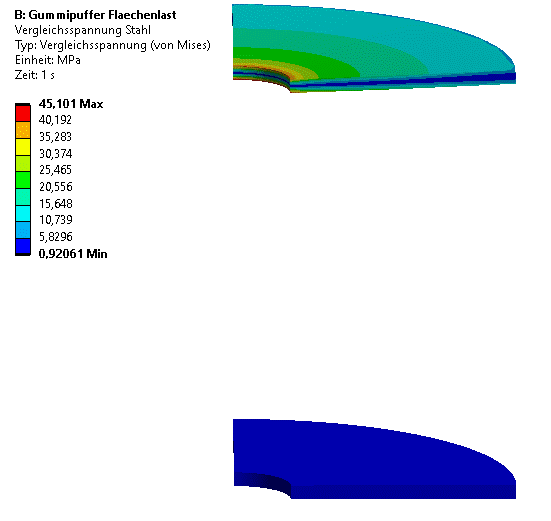
- Die max. Belastung der oberen Stahlscheibe ist ca. um den Faktor 15 geringer als bei der Streckenlast auf der Lochkante.
- Die Verformung der oberen Stahlscheibe ist sehr gering und resultiert aus den Kräften des sich verformenden Gummi.
- Die untere Stahlscheibe wird aufgrund der kompletten Auflage auf der Unterlage nicht verbogen. Die berechnete Belastung ist wesentlich geringer als in der oberen Stahlscheibe.
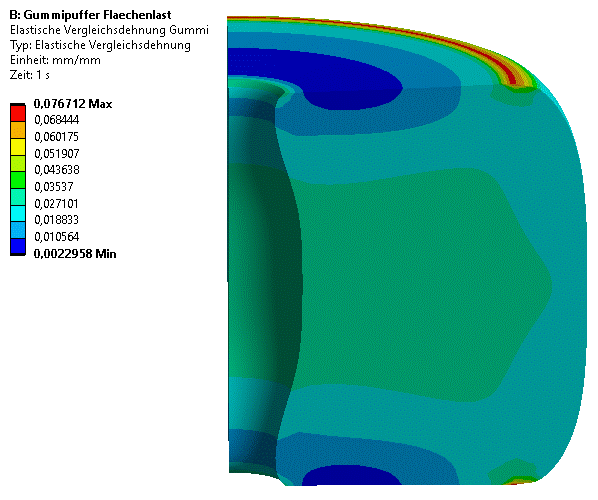
- Im Gummimaterial ist mit Ausnahme der Lochkanten die Belastung ähnlich wie bei der Streckenlast. Die Stahlscheibe zwischen Krafteinleitung und Gummihülse wirkt hier ausgleichend:
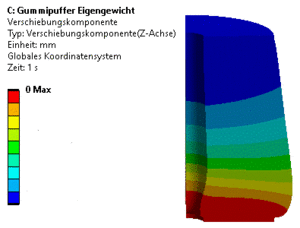
Frage (Deformation):
Wie groß ist die maximale Verformung des Gummipuffers in Z-Richtung für den Lastfall Flächenlast=100 N?
Eigengewicht und Rotation
Um die Verformung in Folge des Eigengewichts und der Rotation nachzuvollziehen, sind zwei duplizierte Studien ("Eigengewicht" und "Rotation") zu erzeugen.
Eigengewicht:
- Kraft-Randbedingung löschen
- MFL > Randbedingungen > Trägheitslasten > Erdanziehungskraft einfügen

- Überprüfen der Richtung
Rotation:
- Kraft-Randbedingung oder Erdanziehungskraft löschen
- MFL > Randbedingungen > Trägheitslasten > Rotationsgeschwindigkeit einfügen
- Drehzahl wie schon in Fusion 360 mit 10.000 U/min definieren
- Richtung entlang der Symmetrieachse des Gummipuffers definieren
- Hinweis: Die Rotationsachse lässt sich auch durch Auswählen einer Mantelfläche definieren.
- Fixierung in Z-Richtung löschen
- konsistent zur Studie in Fusion eine vollständig fixierte zylindrische Lagerung einfügen (MFL > Randbedingungen > Strukturmechanik > Lagerungen > zylindrische Lagerung)
Frage (Deformation):
Wie groß sind die maximalen Verformungen des Gummipuffers in Z-Richtung (entspricht der "Zusammendrückung") für die simulierten Lastfälle?
Thermisch
Unterschiedliche Materialien besitzen unterschiedliche thermische Ausdehnungskoeffizienten. In Abhängigkeit von der aktuellen Temperatur kommt es zu einer Verformung des Bauteils. Die Verformungen führen zu mechanischen Spannungen in den Materialien, welche ihrerseits wieder auf die Verformung zurückwirken. In Form eines weiteren Lastfalls soll die Schrumpfung der Gummihülse nach dem Vulkanisieren untersucht werden:
- Das Vulkanisieren des Gummis an die Stahlscheibe erfolgt bei einer Temperatur von 150°C.
- Bei dieser Temperatur erfolgt der Zuschnitt der Gummihülse auf das Nennmaß der zylindrischen Form.
- Von Interesse ist nun für den unbelasteten Zustand bei 20°C:
- wie sich der Schrumpfungsprozess auf die Form des Puffers auswirkt und
- welche Spannungen im Material infolge der Schrumpfung auftreten.
In Ansys Mechanical lassen sich in der statischen Analyse auch thermische Randbedingungen hinzufügen und so gekoppelte Probleme betrachten. Wir benötigen diese Funktion, weil unsere Symmetrieeigenschaften über mechanische Randbedingungen (Verschiebungen) definiert sind.
- Wir duplizieren die Analyse Rotation (D5) und benennen die Kopie in Thermisch um.
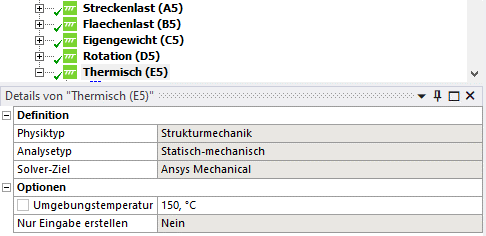
- Wir simulieren wieder den Abkühlvorgang und setzen deshalb die Umgebungstemperatur in den Details von "Thermisch (E5)"' auf 150 °C.
- Die Randbedingungen für Symmetrie und Lagerung können beibehalten werden. Die Rotationsgeschwindigkeit muss man löschen.
- Unter MFL > Randbedingungen > Strukturmechanik > Lasten > Thermische Bedingung
 fügt man die Temperatur-Randbedingung ein.
fügt man die Temperatur-Randbedingung ein. - Es soll wieder eine abgekühlte Endtemperatur von 20 °C an allen drei Körpern vorliegen.
- Der simulierte Temperaturverlauf ist zeitunabhängig, d.h. es wird der Zustand des thermischen "Gleichgewichtes" berechnet.
- Mit diesem Temperaturverlauf kann dann (automatisch) eine elasto-statische Berechnung durchgeführt werden, wobei aus den aktuellen Temperaturwerten unterschiedliche thermische Dehnungen im Material resultieren, welche zu thermo-mechanischen Verschiebungen und Spannungen führen.
Es ergibt sich ein markantes Verformungsbild infolge des stärkeren Schrumpfens des Gummis im Vergleich zum Stahl:
- Die mechanische Belastung des Gummis ist am höchsten an der Außenkante der Stahlscheibe. Infolge der Scherspannung könnte es dort zum Abschälen des Gummi von der Stahlscheibe kommen.
Frage (Deformation):
Wie groß ist die maximale Verformung des Gummipuffers in Z-Richtung infolge des Abkühlens nach dem Vulkanisieren?