Software: FEM - Tutorial - 3D-Mechanik - Ansys - Axialsymmetrie

↑

← →

Axial-symmetrische Volumen-Elemente (2D)

Mit dem Vorgehen zur strukturierten Vernetzung aus der ersten Übung wäre es sicher möglich, das Netz noch zu verbessern. Außerdem könnte man den Gummipuffer in der X-Y-Ebende halbieren und so nur einen Achtel-Puffer simulieren, der sich entsprechend feiner vernetzen lässt. Da die automatische Vernetzung mit Hexaedern aber schon sehr nah an diese optimierten Fälle heran kam, sparen wir uns den Aufwand und probieren noch einen neuen Ansatz aus.
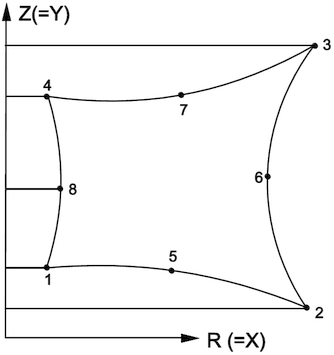
Anstatt eines Viertel- oder Achtel-Zylinders genügt bei Ausnutzung aller Symmetrie-Eigenschaften für den Gummipuffer auch ein Finite-Elemente-Netz in Form eines "unendlich" dünnen Tortenstücks der oberen Pufferhälfte:

• Für die Klasse der rotationssymmetrischen Geometrie wurden spezielle Finite 2D-Elemente (Torus-Elemente) entwickelt.
• Axialsymmetrische Elemente sind 2D-Elemente in Zylinderkoordinaten (Z,R) zum Modellieren von Volumenkörpern, die in Bezug auf Geometrie, Last und Randbedingungen symmetrisch zur Z-Achse sind. Negative R-Koordinaten sind nicht zulässig. Das 2D-Netz entspricht einer Profil-Skizze für das Erzeugen eines Rotationskörpers durch Drehung um die Z-Achse.
• Die "Dicke" dieser 2D-Elemente verläuft entlang eines Kreisbogens, dessen Länge proportional zum Abstand des Elements von der Z-Achse ist.
• Gezeichnet werden für Ansys die Torus-Elemente in der karthesischen XY-Ebene:
  Y-Achse → zylindrische Z-Achse / X-Achse → zylindrischer Radius R

Geometrieskizze

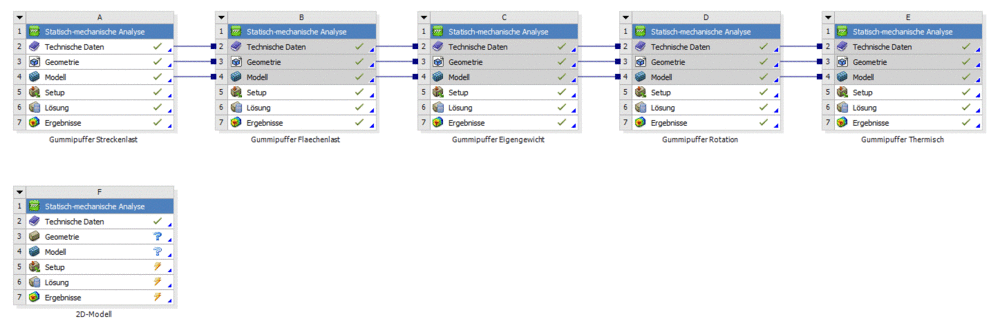
Um die Materialparameter zu übernehmen, wechseln wir in die Workbench und duplizieren dort die Ausgangsanalyse A. Anschließend setzen wir die Geometrie zurück, um diese neu erstellen zu können.

Die einfache Grundgeometrie der Schnittfläche lässt sich gut mit SpaceClaim erstellen:

• Öffnen von SpaceClaim durch Doppelklick auf Geometrie.
• Da 2D-Modelle bei Ansys nur in der XY-Ebene funktionieren, muss man diese für die neue Skizzenebene auswählen.
• Damit später die Materialien Gummi und Stahl den beiden zu erstellenden Flächen zugewiesen werden können, müssen diese Flächen nacheinander definiert werden:
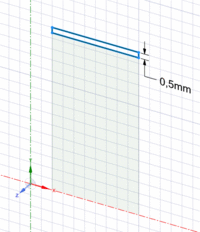
  1. Zeichnen eines Rechtecks über MFL > Skizze > Erstellen > Rechteck mit einer Kante auf der X-Achse und mit Abstand zur Y-Achse.
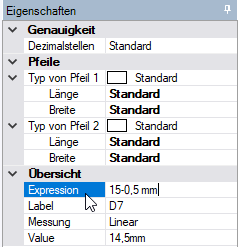
  2. Bemaßen des Rechtecks. Von der Höhe muss dabei die individuelle Scheibendicke abgezogen werden: 15 mm - 0,5xx mm
     
  3. Skizzenbearbeitung beenden über MFL > Skizze > Skizze beenden.
  4. Erneutes betreten des Skizziermodus über MFL > Konstruktion > Modus.
  5. Auswählen der Skizzierebene.
  6. Zeichnen eines Rechtecks, das über dem ersten Rechteck angeordnet ist.
  7. Bemaßen mit einer Höhe von 0,5xx mm (im Bild für Teilnehmernummer 00).
  8. Beenden der Skizze.
  9. Schließen von SpaceClaim.

Hinweis:

• Je nach Teilnehmernummer kann es notwendig sein, für die Höhe des halben Gummipuffers mehr als zwei Nachkommastellen anzugeben.
• Dazu ist es notwendig die Präzision der Skizzenbemaßung zu erhöhen.
• Die entsprechende Einstellung findet man nach Klick auf Datei (oben links in der Menüleiste) in den .
• Dort muss man in der Kategorie Einheiten die Primäre Genauigkeit auf 3 Nachkommastellen erhöhen und mit ok bestätigen.
• Anschließend lässt sich die Skizze auch bei ungeraden Teilnehmernummern korrekt anlegen.

Axialsymmetrisches 2D-Modell

Von der Projektübersicht starten wir Ansys Mechanical, um die weitere Konfiguration des Modells vorzunehmen.

• Die aus SpaceClaim importierten Flächen besitzen noch keine sinnvollen Namen, wenn man nicht vorher schon welche vergeben hat.
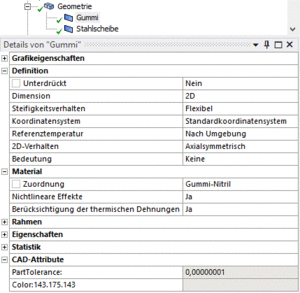
• Spätestens jetzt sollten beide Geometrieobjekte korrekt benannt werden (Stahlscheibe und Gummi).
• Im selben Arbeitsschritt weisen wir den Flächen auch das zugehörige Material zu.
• Es verbleibt weiterhin ein Fragezeichen vor den Geometrieelementen und es soll noch eine Dicke der 3D-Geometrie angegeben werden, die wir eigentlich nicht benötigen. Wir müssen also noch die Axialsymmetrie definieren.
• Unter Details von "Gummi" und Details von "Stahlscheibe" muss die Dimension wieder auf 2D und das 2D-Verhalten auf Axialsymmetrisch umgestellt werden.
• Die vollständige Geometriedefinition sollte jetzt durch einen Haken im Strukturbaum bestätigt werden.

Im Rahmen der grundlegenden Geometriedefinition sollte man eigentlich auch die Verbindungen und Kontakte zwischen den einzelnen Bauteilen definieren. In den bisherigen Analysen konnten wir uns dazu auf die Automatismen von Ansys verlassen. Ein Blick in Kontakte/Verbindungen im Übersichtsbaum zeigt aber, dass für unser aktuelles Modell noch keine Kontakte angelegt wurden. Das liegt daran, dass Kontaktdefinitionen für volumenbehaftete Geometrien mit Oberflächen ausgelegt sind. Es wäre trotzdem möglich, einen Kontakt manuell an den beiden sich berührenden Kanten der Flächen zu definieren. Damit wären später die automatisierten Funktionen der Kontaktvernetzung mit all ihren Features aber auch Einschränkungen zu verwenden. Da wir aber im Folgenden wieder ein hochwertiges strukturiertes Netz anlegen, definieren wir die Kontakte später direkt im fertigen FE-Netz.

Strukturierte Vernetzung

Wenn im Netz noch Steuerelemente durch das Duplizieren der Studie vorhanden sind, sollte man diese zunächst löschen oder weiter nutzen und entsprechend umdefinieren. Für das Netz müssen nun vier Elementgrößen definiert werden. Durch die Spiegelsymmetrie bietet sich eine Verzerrung des Gummi-Netzes in axialer Richtung an. Damit lassen sich die kritischen Bereiche an den Rändern feiner auflösen. Es müssen folgende Steuerungen der Elementgröße angelegt und benannt werden. Die Netzsteuerung betrifft immer das ihrem Namen nach sinnvolle Geometrieelement:

• Elementgröße Gummi radial:
  • Zuweisen der zwei horizontalen Kanten als Geometrie
  • Typ: Elementgröße = 0,05 mm
  • Verhalten: Strikt
  • Verzerrungstyp: - --- ----- --- -
  • Verzerrungsoption: Verzerrungsfaktor = 3
• Elementgröße Gummi axial:
  • Zuweisen der zwei vertikalen Kanten als Geometrie
  • Typ: Elementgröße = 0,1 mm
  • Verhalten: Strikt
  • Verzerrungstyp: ----- --- - -
  • Verzerrungsoption: Verzerrungsfaktor = 6
  • Bei Bedarf muss die Verzerrung von Kanten des Gummis in axialer Richtung umgekehrt werden. Man erkennt schon in der Vorschau anhand der gelben Markierungen, wie die Kanten ausgerichtet sind.
• Elementgröße Stahl radial:
  • Zuweisen der zwei horizontalen Kanten als Geometrie
  • Typ: Elementgröße = 0,05 mm
  • Verhalten: Strikt
  • Verzerrungstyp: - --- ----- --- -
  • Verzerrungsoption: Verzerrungsfaktor = 3
• Elementgröße Stahl axial:
  • Zuweisen der zwei vertikalen Kanten als Geometrie
  • Typ: Elementgröße = 0,04 mm
  • Verhalten: Strikt
  • Verzerrungstyp: Gleichmäßig
• Bevor man das Netz aktualisiert, muss noch die Option Flächenvernetzung hinzugefügt und beide Geometrieflächen zugewiesen werden.
• Aktualisieren des Netzes.

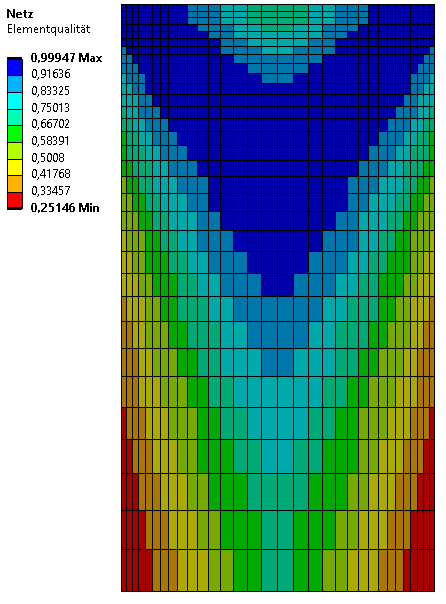
Wir erhalten ein hochaufgelöstes Netz mit sehr guter Qualität, insbesondere in den kritischen Bereichen. Dass die Qualität in der Mitte der Gummihülse aufgrund des axialen Verzerrungsfaktors (6) geringer ausfällt, stellt kein Problem dar. Wir wissen, dass hier keine kritischen Spannungen auftreten und haben die konkreten Werte in diesem Bereich nie betrachtet. Aufgrund des 2D-Ansatzes kommt das Netz trotzdem mit nur 25.000 Knoten aus. Würde man wie im 3D-Fall quadratische Elemente mit Mittelknoten nutzen, käme man mit 75.000 Konten auf eine deutlich höhere Anzahl, die für die Auflösung aber weiterhin sehr gut ist.
Hinweis: Das abgebildete Netz ist zur besseren Sichtbarkeit um den Faktor 5 gröber. Qualitativ sollte sich der gleiche Aufbau mit höherer Auflösung ergeben.

Spätestens beim Starten der Simulation würde jetzt auffallen, dass im 2D-Modell kein automatischer Kontakt zwischen Stahlscheibe und Gummi hergestellt wird. Da unser strukturiertes Netz an beiden Körpern genau aufeinander passt, greifen wir hier auf die Option Knotenverschmelzen zurück:

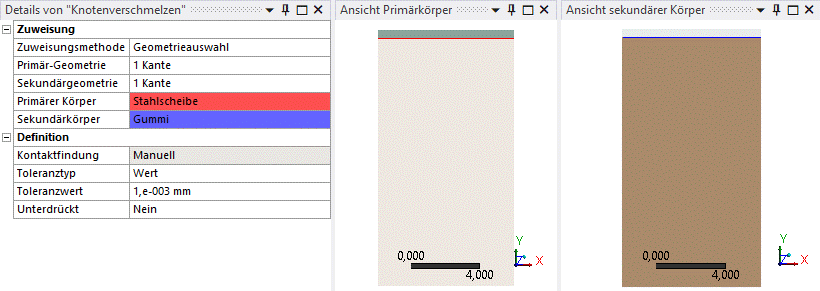
• Über das Kontextmenü von Projekt > Modell > Netz kann man mit Einfügen > Knotenverschmelzen nahe beieinander liegende Knoten vereinen.
• Als Primär-Geometrie wählen wir die Unterkante der Stahlscheibe aus.
• Sekundär-Geometrie ist die Oberkante des Gummis.
• Bei der Auswahl der Kanten kann das Ein- und Ausblenden bzw. Invertieren der Flächensichtbarkeit (Körper) helfen. Es ist wichtig in den Details von "Knotenverschmelzen" und im Grafikbereich zu überprüfen, dass die Kanten beider Körper korrekt zugewiesen sind:

• Da wir nur die Knoten auf der Kante verbinden möchten, setzen wir den Toleranzwert auf 0,001 mm.
• Zuletzt muss über das Kontextmenü von Projekt > Modell > Netz bearbeiten > Knotenverschmelzen-Gruppe > Knotenverschmelzen die Option Erstellen angeklickt werden, um die Verschmelzung anzuwenden.

Hinweis: Die verschmolzenen Knoten ergeben automatisch einen Kontakt vom Typ "Verbund". Für unseren Fall ist das genau das angestrebte Verhalten. Möchte man aber die anderen Kontaktarten verwenden (z.B. mit Reibeffekten), so dürfen die Einzelnetze natürlich nicht einfach verschmolzen werden.

Randbedingungen definieren

Falls nach dem Duplizieren noch Randbedingungen und Lasten aus der 3D-Analyse vorhanden sind, sollte man diese löschen. Es fehlt nur noch die Randbedingung für die Symmetrie um die X-Achse (R-Achse), da Punkte auf der Y-Achse (Z-Achse des Zylinder-Koordinatensystems) bereits infolge der Torus-Elemente als unverschieblich in in R-Richtung definiert sind:

• Eine Symmetrie-Bedingung muss die Verschiebung der Knoten auf der Schnitt-"Fläche" in Z-Richtung des Zylinder-Koordinatensystems verhindern. Dies entspricht der Verschiebung in Y-Richtung des verwendeten XYZ-Koordinatensystems!
• Dazu nutzt man am besten eine Verschiebung-Randbedingung, die man sinnvollerweise "Symmetrie XZ-Ebene" nennt.
• Hinweise:
  • Linien eines axialsymmetrischen Netzes aus Torus-Elementen repräsentieren infolge der "gedachten" Rotation um die Z-Achse immer Flächen um die Z-Achse des Zylinder-Koordinatensystems.
  • Beim Starten der Lösung kommt es vermutlich zu einer Warnung, die besagt, dass nicht genügend Randbedingungen definiert wurden. Wie dort beschrieben, prüfen wir die Ergebnisse sorgfältig. Wenn alles den Erwartungen entspricht, wird klar, dass diese Warnung auf die fehlenden Bedingungen abzielt, die implizit über die Definition der Achssymmetrie gegeben sind, scheinbar aber nicht in Mechanical überprüft werden.

Streckenlast auf Lochkante

Die Lochkante wird nur durch einen Eckknoten der Stahlscheibe repräsentiert:

• Der Gummipuffer soll wieder mit einer Druck-Kraft von 100 N auf dieser Lochkante belastet werden (nicht als "Druck"!).
• Achtung: Ansys nimmt bei Axialsymmetrie an, dass das Bauteil die vollen 360° umfasst und behandelt Lasten entsprechend:

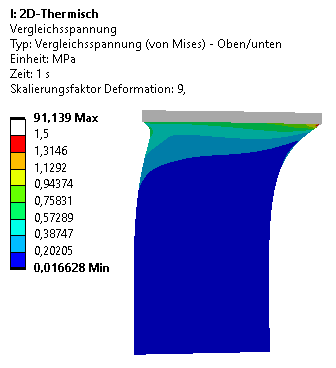
• Infolge der feinen Vernetzung zeigen die Spannungsverläufe mehr Details.
• Die höchsten Belastungen des Gummimaterials treten an den Kanten zur Stahlscheibe auf.
• Bei reiner Streckenlast auf der Lochkante wird die Stahlscheibe in der Mitte relativ stark verformt. Dies führt zu einer erhöhten Belastung des Gummis im Innern.

Flächenlast auf Stahlscheibe

Für den zweiten Lastfall kann man wieder innerhalb von Ansys Mechanical duplizieren.

Die Oberseite der Stahlscheibe wird durch die obere Kante des Netzes repräsentiert:

• Der Gummipuffer soll mit einer Kraft von 100 N gleichmäßig auf dieser Fläche belastet werden:

• Die Stahlscheibe wird bei Flächenbelastung bedeutend weniger verformt, was auch die Belastung des Gummis ändert.
• Insbesondere wird das Gummimaterial an der Lochkante der Stahlscheibe nicht mehr sehr stark belastet.

Thermische Last

Auch in der 2D-Analyse sind thermische Studien möglich. Dazu kann man eine der vorgelagerten Studien duplizieren.

• Die Umgebungstemperatur zu Beginn beträgt wieder 150°C.
• Beide Körper sollen über eine thermische Randbedingung auf 20°C abgekühlt werden.
• Hinweis: Die Thermische Bedingung lässt sich nur auf Körper als Geometrie anwenden. Man muss die beiden Flächen also mit dem korrekten Auswahlwerkzeug (<Strg+B>) anklicken, damit sie von der Randbedingung akzeptiert werden.
• Die Kraft wird als Last nicht mehr benötigt.

• Auch hier sind die berechneten Verläufe detaillierter als in der 3D-Analyse.

Fragen

1. Wie groß sind die Maximalwerte der Mises-Spannung des Gummipuffers direkt an der Stahlscheibe und im Innern des Gummimaterials für die drei Lastfälle?
2. Wie stark wird der Gummipuffer maximal in Längsrichtung bei den beiden Lastfällen zusammengedrückt?
3. Die erhaltenen Werte sind mit den Ergebnissen aus der Autodesk-Fusion-Simulation und dem Ansys-3D-Modell zu vergleichen.
4. Welchen Ergebnissen kann man am meisten vertrauen? Die Aussage ist zu begründen!

← →