Software: FEM - Tutorial - 3D-Mechanik - Ansys - nichtlineare Deformation

↑

← →

Nichtlineare Deformation

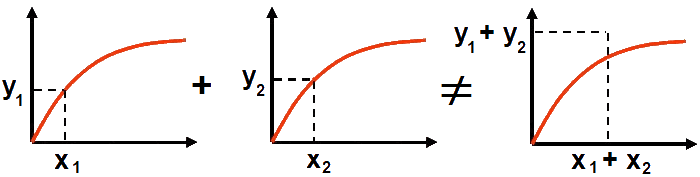
Für lineare Systeme gilt das Superpositionsprinzip:

• Wirken gleichzeitig mehrere Eingangsgrößen x_i (Lastwerte), so ergeben sich die Lösungen für die Ergebnisgrößen y_n als Summe der Wirkung der einzelnen Eingangsgrößen.
• Voraussetzung ist eine lineare Übertragungsfunktion Y=f(X) zwischen allen Eingangsgrößen und den berechneten Ergebnisgrößen.
• Für umfangreiche lineare Gleichungssysteme hat dies den Vorteil, dass nicht für jeden Lastfall das Gleichungssystem neu gelöst werden muss, da man anhand von Proportionalitäten die skalierten Ergebnisse eines Lastfalls nutzen kann.

Nichtlineare Systeme → das Superpositionsprinzip gilt nicht:

Bei Finite-Element-Modellen kann man drei grundsätzliche Ursachen der Nichtlinearität unterscheiden:

1. Material-Nichtlinearität = Abhängigkeiten der Materialparameter von berechneten Ergebnisgrößen, z.B. in der Strukturmechanik:
   • E-Modul bleibt nicht konstant infolge einer nichtlinearen Spannungs-Dehnungs-Kurve.
   • Eine sich ändernde Spannungs-Dehnungskurve-Kurve (Hysterese) durch Plastizität.
2. Geometrie-Nichtlinearität = Auftreten von Verschiebungen quer zur Lastrichtung (in der Strukturmechanik):
   • Mit Ausnahme von Stab-Elementen treten infolge von Querkontraktion in FE-Modellen immer Verschiebungen quer zur Lastrichtung auf.
   • Wirkt die Struktur als ebener bzw. räumlicher Bewegungswandler (z.B. z=f(x,y)), ist die Übersetzung der Bewegung durch nichtlineare trigonometrische Terme gekennzeichnet.
   • Für kleine Auslenkungen (z.B. kleiner als die Wanddicke des Bauteils) kann man geometrische Nichtlinearität meist vernachlässigen.
   • Im Bauwesen schreiben Normen vor, geometrische Nichtlinearitäten zu berücksichtigen, wenn die Verformungen dadurch um mehr als 10% zunehmen!
3. Strukturnichtlinearität = Umschalten des Verhaltens von Modellbereichen bei bestimmten Ereignissen:
   • Kontakt-Nichtlinearität in der Strukturmechanik bei Verformung (Siehe: Baugruppenbehandlung in FE-Modellen)
   • Der Kontaktsolver behandelt nur die Unstetigkeiten der Kontaktstellen. Die Simulation der Bauteile erfolgte unabhängig davon im Übungsbeispiel als lineare Systeme.

Geometrische Nichtlinearitaet

Die strukturierten vernetzten FE-Modelle des Gummipuffers berechneten wir bisher nur mit der Analyseeinstellung des Solvers Große Verformung = Aus (entspricht der empfohlenen Vorgehensweise):

• Die linearen Ergebnisse ermöglichen eine Validierung des Modells und vermitteln einen Eindruck zum Bauteilverhaltens.
• Falls (wie in unserem Beispiel) nicht nur "unmerkliche" Verformungen auftreten, sollte man als nächstes die geometrischen Nichtlinearitäten in die Simulation einbeziehen.

Wir behandeln die Einbeziehung der Nichtlinearitäten nur am Beispiel des 2D-axialsymmetrischen Modells mit Streckenlast:

• Analysemodell mit strukturiertem Netz und Streckenlast erneut duplizieren.
• Umbenennen in "Streckenlast grosse Verformung".
• Unter Details von "Analyseeinstellungen" aktivieren wir nun die Große Verformung und damit die Betrachtung geometrischer Nichtlinearität.
• Startet man jetzt die Lösung, läuft diese ohne detaillierte Rückmeldung durch und man erhält die gewohnten Ergebnisse.
• Bei genauer Betrachtung fällt aber auf, dass die Verschiebung in axialer Richtung (Kompression) etwa 3% kleiner ist als im linearen Fall, obwohl sonst keine Einstellung geändert wurde.
• Dieses Verhalten erklärt sich dadurch, dass die Streckenlast im Laufe der Simulation verkippt und damit bei zunehmender Verformung einen kleineren Beitrag in Y-Richtung leistet. Bei der linearen Analyse wurde dies vernachlässigt.
• Für die Flächenlast wäre dieser Vergleich weniger deutlich, weil hier keine so starke Verkippung des Kraftvektors auftritt.
• Ein Blick in die detaillierten Lösungsinformationen des Solvers zeigt, dass intern 3 Iterationen zur numerischen Lösung des nichtlinearen Problems durchlaufen wurden. Das war vorher nicht der Fall:

    DISP CONVERGENCE VALUE   =  0.4735      CRITERION=  0.2416E-01
   EQUIL ITER   1 COMPLETED.  NEW TRIANG MATRIX.  MAX DOF INC= -0.4735    
    FORCE CONVERGENCE VALUE  =   2642.      CRITERION=  0.5235    
    DISP CONVERGENCE VALUE   =  0.1396E-01  CRITERION=  0.2465E-01 <<< CONVERGED
   EQUIL ITER   2 COMPLETED.  NEW TRIANG MATRIX.  MAX DOF INC=  0.1396E-01
    FORCE CONVERGENCE VALUE  =  0.8759      CRITERION=  0.5332    
    DISP CONVERGENCE VALUE   =  0.1412E-02  CRITERION=  0.2515E-01 <<< CONVERGED
   EQUIL ITER   3 COMPLETED.  NEW TRIANG MATRIX.  MAX DOF INC=  0.1412E-02
    FORCE CONVERGENCE VALUE  =  0.3439      CRITERION=  0.5441     <<< CONVERGED
   >>> SOLUTION CONVERGED AFTER EQUILIBRIUM ITERATION   3

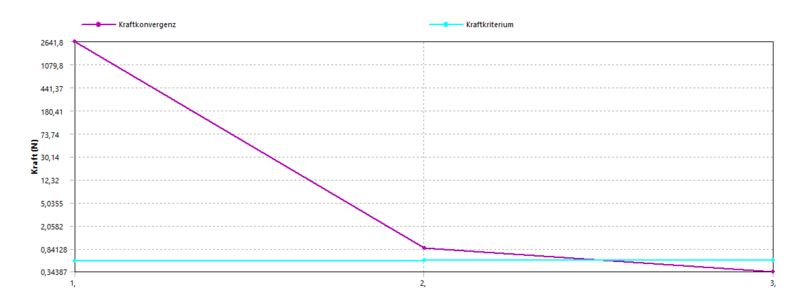
• In den Details von "Lösungsinformationen" lassen sich die Konvergenzkriterien auch einzeln auswählen und grafisch darstellen.
• Die Konvergenzkriterien werden als Qualitätsmerkmal der Näherungslösung genutzt. Die Funktion lässt sich z.B. am Kraftkriterium gut erklären:
  • Theoretisch sollte die Summe aller Kräfte im FE-Modell immer exakt 0 sein.
  • Aufgrund numerischer Ungenauigkeiten trifft das nicht ganz zu.
  • Bei nichtlinearen Berechnungen mit zu großer Schrittweite wird dieser Effekt dadurch verstärkt, dass das Superpositionsprinzip nicht mehr gilt.
  • Im Konvergenzkriterium wird überprüft, dass nach dem jeweiligen Iterationsschritt die Gesamtkraft kleiner als der gesetzte Schwellwert ist.
  • Wird das Kriterium nicht erfüllt, muss ein zusätzlicher Zwischenschritt durchgeführt werden. So ergeben sich im Beispiel 3 Iterationen:

In den Einstellungen der Nichtlinearen Steuerung unter Details von "Analyseeinstellungen" verstecken sich eine Vielzahl von Optionen, die man detailliert in der Produktdokumentation nachvollziehen kann. Im Allgemeinen bleibt man zunächst überall bei der Einstellung Programmgesteuert und ändert diese nur dann, wenn Probleme auftauchen. Hier soll ein ausgewählter Aspekt erläutert werden:

• Das bisherige Vorgehen, bei dem auch in der nichtlinearen Simulation nur ein Lastschritt berechnet wird, entspricht dem "Full" Newton-Raphson-Verfahren (sofort volle Last-Amplitude).
• Dieses Verfahren stößt bei stark nichtlinearen Problemen an seine Grenze und konvergiert nicht.
• Das Inkrementellen Newton-Raphson-Verfahren erzwingt man in Ansys, indem man die Zeitschrittsteuerung aktiviert.
• Dazu unter Details von "Analyseeinstellungen" > Schrittsteuerung > Automatische Zeitschrittsteuerung > Ein wählen.
• Anhand der Substeps kann man jetzt definieren, wie viele Zwischenschritte echt berechnet werden sollen.
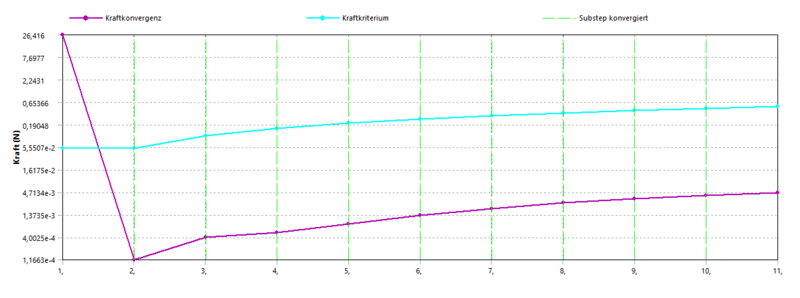
• Bei der Berechnung von 10 Einzelschritten bis zum Aufbringen der vollständigen Belastung benötigt die erste Berechnung, wegen der kleineren Kraft nur noch zwei Iterationen. Alle weiteren Lastschritte konvergieren sofort:

• Der Maximalwert der Kraftkonvergenz zeigt sehr anschaulich, dass im ersten Schritt jetzt nur 10% der Gesamtkraft aufgebracht werden.
• Beim Abspielen einer Animation hat man jetzt die Wahl zwischen der interpolierten Animation (grün) und der Anzeige der echt berechneten Ergebnissätze (blau) :

• Bei den dargestellten Lastschritten handelt es sich um wirklich berechnete Ergebnisse, nicht um eine lineare Interpolation zwischen Anfangs- und Endzustand, wie wir sie aus der Belastungsanimation mittels Autodesk Fusion 360 kennen.

• Für die abzugebende Lösung muss die Automatische Zeitschrittsteuerung unbedingt wieder auf Programmgesteuert zurückgestellt werden. Dadurch lässt sich die Größe der Lösungsdatei reduzieren.

Fragen

Im Vergleich zu den linearen Ergebnissen des 2D-Axialmodells für die Streckenlast sind folgende Werte zu analysieren:

1. Wie stark wird der Gummipuffer maximal in Längsrichtung zusammengedrückt?
2. Wie groß sind die Maximalwerte der Mises-Spannung direkt an der Stahlscheibe und im Innern des Gummimaterials für die maximale Belastung?
3. Wie groß ist die prozentuale Abweichung für diese Werte?

← →