Software: FEM - Tutorial - 3D-Mechanik - Ansys - nichtlineare Materialeigenschaften

↑

← →

Nichtlineare Materialeigenschaften

Hintergrundinformationen

Die Berücksichtigung der geometrischen Nichtlinearität führte im Beispiel zu geringfügigen Verbesserung der Ergebnisse. Dabei wurde mit konstantem E-Modul für die Materialien gerechnet:

• Unter dem Punkt Geometrie in den Details von "Gummi" kann man sehen, dass für das gewählte Material die Nichtlinearen Effekte auf Ja stehen. Da wir diese komplexen Eigenschaften für unser Nitril-Gummi nie hinterlegt haben, bleibt die Einstellung ohne Effekt.

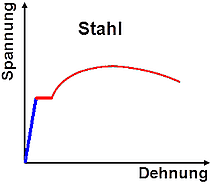
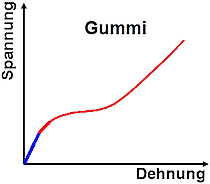
• Standardmäßig ist nach Zuweisung der Materialien das Hookesche Gesetz mit konstantem E-Modul und konstanter Querkontraktionszahl aktiviert (blauer Bereich kleiner Dehnung in nebenstehenden Spannungs-Dehnungs-Diagrammen).
• Bleiben diese "Konstanten" infolge der Belastung nicht konstant, so kann man in der Strukturmechanik drei Haupttypen von Materialnichtlinearitäten unterscheiden:

1. nichtlinear-elastisches Verhalten:
   
   • die Dehnungen sind nicht proportional zu den Spannungen,
   • die Be- und Entlastung folgt der gekrümmten Funktion σ=f(ε),
   • innere Verluste werden nicht berücksichtigt → keine Hysterese zwischen Be- und Entlastung (unterer roter Bereich im Gummi-Diagramm).
2. Plastizität:
   • Belastung und anschließenden Entlastung ergibt bleibende plastische Dehnungen (roter Bereich im Stahl-Diagramm),
   • Zusätzlich zum Spannungs-Dehnungs-Diagramm σ=f(ε) ist eine Fließkurve σ_f=f(ε_pl) erforderlich, welche z.B. durch Wertepaare aus plastischer Dehnung und zugehöriger Spannung definiert wird.
   • innere Verluste → Hysterese zwischen Be- und Entlastung
   • Kriechen als zeitabhängige Komponente muss separat beschrieben werden
3. Hyperelastizität:
   • inkompressibles, rein elastisches Materialverhalten (Querkontraktionszahl=0,5)
   • E-Modul wird größer bei großer Dehnung,
   • bei hyperelastischen Materialien (z.B. Gummi) bis zu mehreren Hundert Prozent Dehnung möglich (oberer roter Bereich im Gummi-Diagramm),
   • treten große Dehnungen tatsächlich auf, so werden Finite Elemente stark verzerrt (ist bei der Vernetzung, der Elementwahl und im Solver zu berücksichtigen!).

Bei der Berücksichtigung nichtlinearer Materialeigenschaften existieren zwei grundsätzliche Probleme:

1. Verfügbare Materialgesetze im verwendeten FEM-Programm:
   • Die implementierten Zusammenhänge sind immer Idealisierungen, die für Metall-Werkstoffe meist hinreichend genau die wesentlichen Abhängigkeiten berücksichtigen können.
   • Für Kompositwerkstoffe und Kunststoffe trifft dies häufig nicht mehr zu.
   • In der Ansys-Studentenversion sind einige "Kostproben" komplexer Materialmodelle enthalten. Umfangreiche Datenbanken für den professionellen Einsatz sind im Allgemeinen kostenpflichtig.
2. Beschaffung der "richtigen" Material-Kenngrößen:
   • Meist ist man auf eigene Messungen für verwendete Materialien angewiesen, weil die erforderlichen nichtlinearen Zusammenhänge vom Hersteller nicht geliefert werden oder für den Einsatzbereich nicht gültig sind (z.B. starke Temperatur-Abhängigkeit bei Elastomeren).
   • Der prozentuelle Fehler von Material-Kenngrößen führt zu ähnlichen großen Fehlern in den Simulationsergebnissen. Der Ersatz des zuvor als konstant angenommenen E-Moduls durch eine Kennlinie garantiert also nicht automatisch genauere Lösungen.

Beispiel: "Gummipuffer" in den bisherigen Studien

1. Stahlscheiben:
   • Dürfen nur im elastischen Bereich betrieben werden!
   • Die erforderliche Information erhält man durch die Ermittlung des Sicherheitsfaktors auf Grundlage der zulässigen Spannung.
   • Unterhalb dieser zulässigen Spannung gilt das Hooke'sche Gesetz und die Berücksichtigung nichtlinearer Materialeigenschaften ist nicht erforderlich.
2. Gummihülse:
   • Nur an den Kanten zu den Stahlscheiben treten relativ große Dehnungen auf.
   • Da für das verwendete Gummimaterial keine konkreten Kennlinien zur Verfügung stehen, kann man sich auch hier auf die Überprüfung zulässiger Spannungswerte beschränken.

Bei einfachen Materialmodellen ist der elastische Anteil der Dehnung immer durch einen konstanten E-Modul definiert (blauer Abschnitt des kompletten Spannungs-Dehnungs-Diagramms):

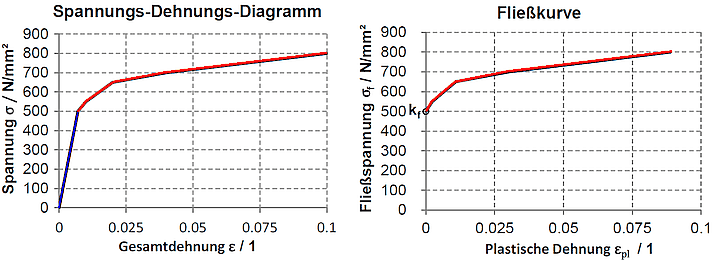
Der Beginn der "Fließkurve" (roter Kurvenbereich) ist definiert durch die Streckgrenze k_f. Es gilt:
.
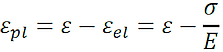Die Punkte der Fließkurven-Streckenabschnitte werden durch Wertepaare (ε_pl, σ_f) als nichtlineare Eigenschaft definiert.

Studie in Ansys Mechanical

Im Folgenden möchten wir die nichtlinearen Eigenschaften eines "echten" Gummis aus den mitgelieferten Materialdatenbanken von Ansys testen:

• Wir schließen die bisherigen Studien in Mechanical und wechseln in die Workbench.
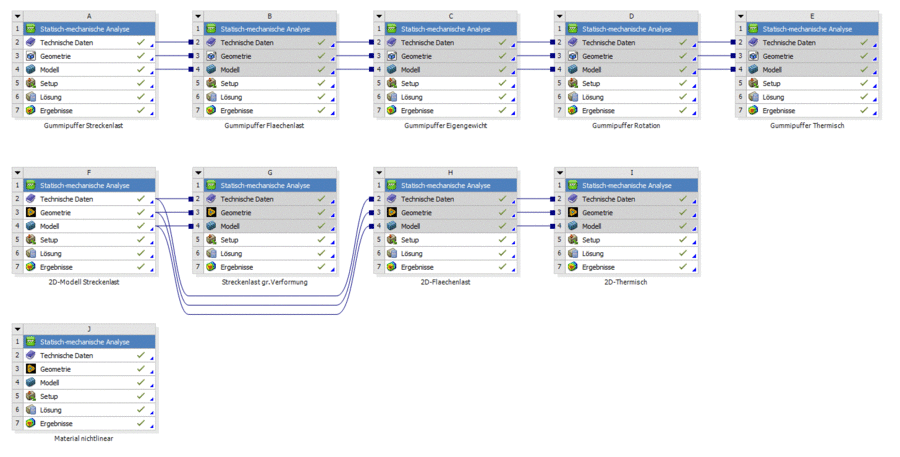
• Zur Übernahme der Geometrie duplizieren wir dort das strukturierte 2D-Modell mit Streckenlast. Bei Vorgehen nach Anleitung ist das Analyse F, von der wir die übrigen 2D-Studien abgeleitet haben.
• Nach dem Duplizieren erhalten wir Studie I, die wir in "Material nichtlinear" umbenennen:

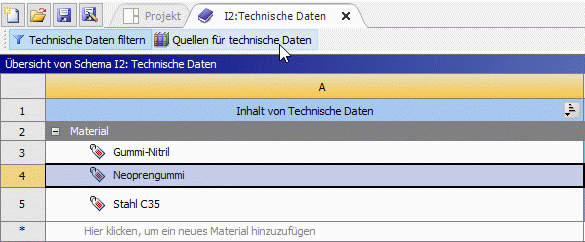
• Nach dem Öffnen der Technischen Daten sehen wir die manuell definierten Materialien Stahl C35 und Gummi-Nitril:

• Um den im Bild schon hinzugefügten Neoprengummi in der eigenen Studie zu ergänzen, öffnet man die Quellen für technische Daten am oberen Bildschirmrand.
• Es öffnet sich eine Tabellenübersicht verschiedener Datenquellen.
• Wir klicken auf Hyperelastische Materialien in Zeile 10.
• In einer weiteren Tabelle der enthaltenen Daten ist der letzte Eintrag der gesuchte Neoprengummi.
• Mit dem Hinzufügen-Button übernehmen wir eine lokale Kopie in unsere Studie. Die Quelle für technische Daten kann man anschließend über die Schaltfläche am oberen Rand wieder verbergen.
• Öffnet man die Eigenschaften des neu hinzugefügten Materials, findet man keine "klassischen" Materialparameter vor.
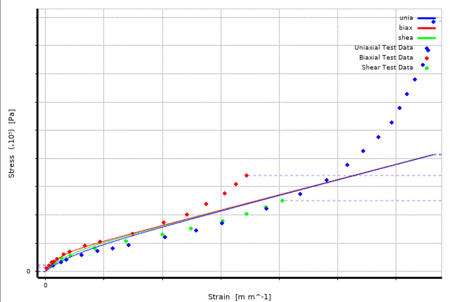
• Wie oben beschrieben ergibt sich das Materialverhalten aus konkreten Versuchsdaten, die als Spannungs-Dehnungs-Kurve hinterlegt sind.
• Für kleinere Dehnungen (unter 200%) lassen sich diese Messwerte mit einem hyperelastischen Materialmodell, dem sogenannten Neo-Hooke-Modell, annähern.
• Diese komplexen Materialmodelle sind mit dem linearen Ansatz nicht direkt vergleichbar.
• Zur Orientierung kann man aus dem Diagramm trotzdem anhand des Anstiegs den "globalen E-Modul" abschätzen:
  • Neoprengummi: ca. 0,5 MPa
  • bisheriger Nitril-Gummi: 12 MPa
• Die nachfolgende Untersuchung demonstriert also lediglich das nichtlineare Verhalten als Übung. Eine konkrete Aussage über unsere bisherige Baugruppe wird sich nicht ableiten lassen.

Nachdem das Material übernommen wurde, können wir von der Projektübersicht aus wieder Ansys Mechanical für die aktuelle Analyse starten.

• Zunächst sollte man im Strukturbaum unter Geometrie dem Gummikörper das neue Material Neoprengummi zuweisen.
• Das Material ist deutlich weicher als der in den vorangegangenen Analysen betrachtete Nitril-Gummi. Die bisher genutzten 100 N würden das Bauteil völlig zerquetschen und stellen durch die starke Verzerrung ein sehr fortgeschrittenes Simulationsproblem dar.
• Wir reduzieren die Streckenlast auf 5 N.
• Die anschließende Lösung des Problems kann je nach PC mehrere Minuten in Anspruch nehmen.
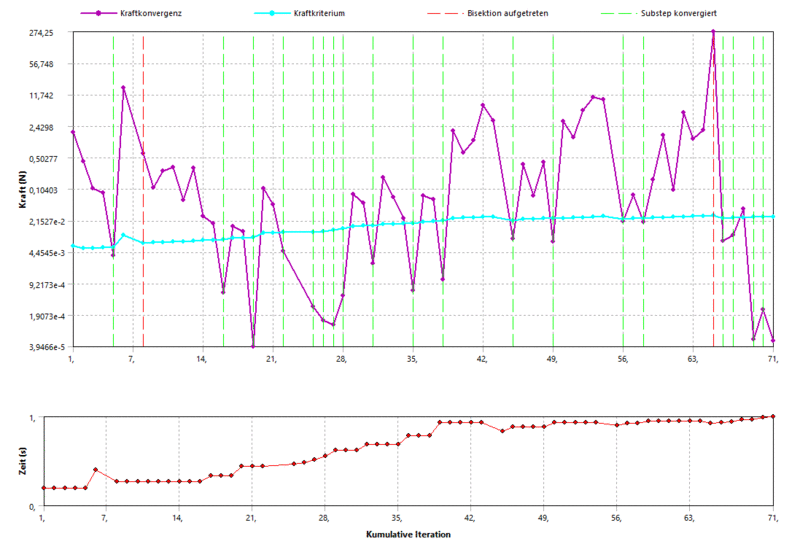
• Die Ursache dafür zeigt sich wieder deutlich am Beispiel der Kraftkonvergenz:

• Der Solver kommt bei der Lösung dieses Problems offenkundig deutlich stärker ins "Schwitzen" als bisher.
• In dieser Studie treten jetzt zum ersten Mal sogenannte Bisektionen auf, bei denen der Solver den aktuellen Iterationsschritt verwirft und es mit einem kleineren Sprung erneut versucht.
• Erkennbar ist das auch daran, dass im Zeitdiagramm (rot) mehrfach zurückgesprungen wird.
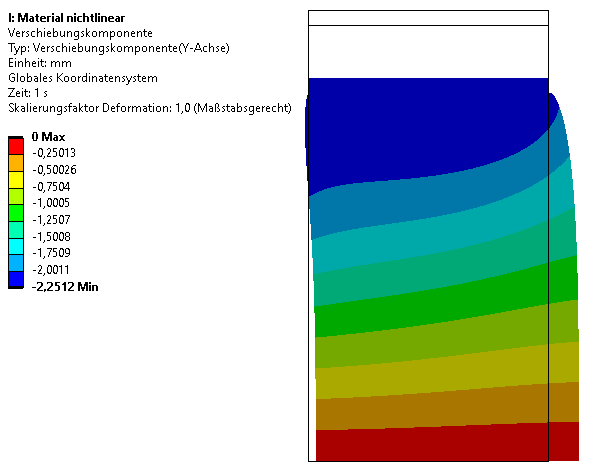
• Etwas anschaulicher zeigen die Simulationsergebnisse das Problem:

• Die Verformung ist mit 2,5 mm sehr groß und entspricht etwa 15% unserer Pufferhöhe (Abbildung ist nicht skaliert!).
• Während der Simulation muss also neben den Nichtlinearitäten des Materials auch eine große geometrische Verformung und die starke Verzerrung der finiten Elemente behandelt werden.
• Interessanterweise sorgt das deutlich weichere Gummi-Material dafür, dass die Stahlscheibe trotz Streckenlast kaum verkippt.
• Dieses Verhalten ist logisch, weil das neue Material mit seiner geringen Steifigkeit keine ausreichende Gegenkraft erzeugen kann, um die starre Stahlscheibe im annähernd selben Maße wie das Gummi zu verformen. (Zuvor haben wir immer übertriebene Skalierungen der realen Verformung betrachtet.)

• Achtung: Vor Abgabe der Datei ist die Kraft in der nichtlinearen Simulation auf 0,5 N zu reduzieren und erneut zu simulieren! Die Ergebnisdatei wird dadurch um etwa 150 MB kleiner! Lösungen, in denen die letzte Studie größer als 50 MB ist, werden nicht akzeptiert!

← →