Software: FEM - Tutorial - 3D-Mechanik - Ansys - FEM-Import

↑

← →

Import in Ansys Mechanical

Export der CAD-Modelle unter Beruecksichtigung der Symmetrie

Im Rahmen dieser Übung soll keine asymmetrische Belastung des Gummipuffers in Bezug auf seine Längsachse stattfinden (z.B. keine schräge Kraftwirkung):

• Unter diesen Bedingungen kann man die Symmetrie-Eigenschaften der Geometrie und der Randbedingungen ausnutzen, um das FEM-Modell zu reduzieren. In der ersten Übung wurde diese Symmetrie-Ausnutzung bereits am Beispiel eines 2D-Modells der Lasche angewandt.
• Um Rechenzeit zu sparen, können wir uns in einem 3D-FEM-Modell auf einen Viertelkreis-Zylinder des Gummipuffers beschränken.
• Die beabsichtigte Simulation des Eigengewichts verhindert eine weitere Reduktion z.B. nur auf die obere Hälfte des Viertelkreis-Zylinders, weil obere und untere Hälfte durch das Gewicht unterschiedlich belastet werden!

Bevor wir die reduzierte Geometrie als STEP-Datei exportieren können, müssen wir temporär mittels einer geeigneten Extrusion deren Form entsprechend beschneiden:

• Dazu wechseln wir im Autodesk Fusion in den "Arbeitsbereich Konstruktion" und wählen dort den kompletten Gummipuffer für die Bearbeitung.
• Die erforderliche Skizze erstellen wir auf der Oberfläche der oberen Stahlscheibe. Danach befinden wir uns im Skizzen-Modus.
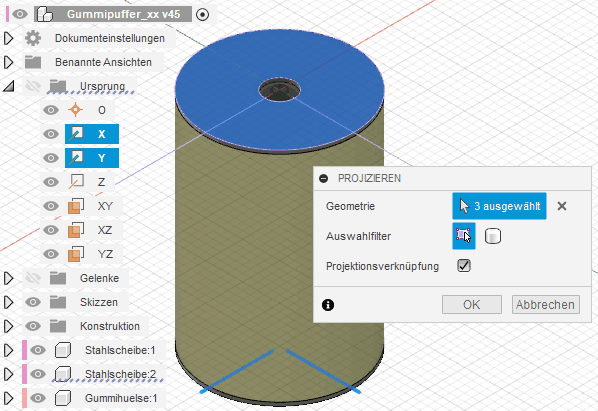
• Erstellen > Projizieren ermöglicht durch Auswahl der Scheibenfläche und der beiden Ursprung-Achsen X und Y die Generierung der erforderlichen Begrenzungen für das Viertel-Profil auf der Skizze:
  
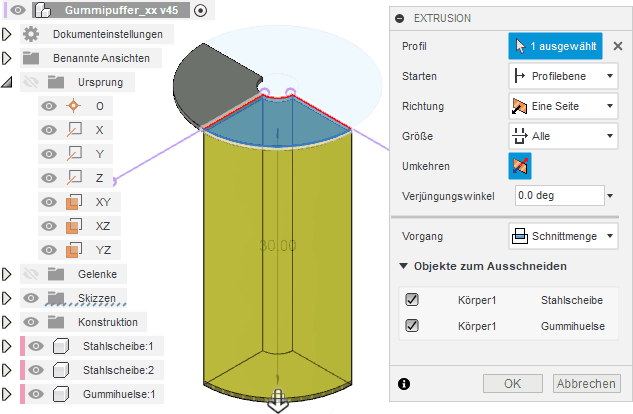
• Bei der Extrusion dieses Viertel-Profils sollte man die Mengenoperation "Schnittmenge" benutzen, um ausgehend von der oberen Stahlscheibe einen Viertelkreis-Zylinder des Gummipuffers zu erzeugen:
  
• Wenn man zu Beginn der Übung die Rotation mit erfasst hat, erscheint das Ergebnis in Hinblick auf die obere Stahlscheibe etwas seltsam, lässt sich jedoch als ein "Feature" von Autodesk Fusion erklären:
  • Geometrie-Änderungen innerhalb einer Konstruktion wirken primär nur auf die Original-Komponenten.
  • Änderungen an Kopien der Original-Komponenten (hier obere Stahlscheibe) entstehen sekundär durch Aktualisieren des Kopierprozesses. Dieser führt im Beispiel durch die enthaltene 180°-Drehung zu einer ungeplanten Verdrehung des oberen Scheiben-Viertels.
  • Hinweis: Wenn das Verhalten wie im Bild auftritt, so muss man die Scheibe durch einen zusätzlichen Verschieben/Kopieren Befehl wieder in die richtige Position bringen.

Die reduzierte Baugruppengeometrien exportieren wir als Gummipuffer_xx.step in den aktuellen Projekt-Ordner:

• Wichtig: Vor dem Speichern der Konstruktionsdatei muss man die Extrusionsskizze (umfasst auch die nachfolgende Extrusion) in der Zeitleiste unterdrücken, um die bisherigen Simulationen nicht zu zerstören!

Import in Ansys

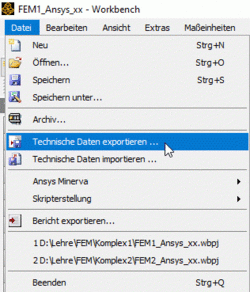
Wie schon in Fusion möchten wir auch hier die Möglichkeit nutzen, unser bereits definiertes Material Stahl C35 weiterzuverwenden. Dazu starten wir zunächst das Projekt der ersten Übung "FEM1_Ansys_xx.wbpj". In der Projektübersicht öffnet man die Technischen Daten einer beliebigen Studie (z.B. A) mit Doppelklick. Sobald sich das Unterfenster öffnet, lässt sich die Konfiguration über Datei > Technische Daten exportieren ... als xml-Datei speichern. Speicherort und Dateiname sollte man sich merken. Das alte Projekt kann man schließen.

Wir erstellen anschließend ein neues Worbench-Projekt und speichern es als "FEM2_Ansys_xx" (mit xx = Teilnehmernummer) im Projektordner des zweiten Übungskomplexes.

Innerhalb des Projekts erstellen wir eine neue Statisch-mechanische Analyse und benennen diesen ersten Anlauf als "Gummipuffer". Nun müssen nach dem bekannten Schema zuerst wieder die Materialdaten hinterlegt werden:

• Dazu öffnet man die Technischen Daten.
• Analog zum Export lassen sich jetzt Datei > Technische Daten importieren ....
• Wir wählen die zuvor gespeicherte xml-Datei mit den Materialdaten.
• In der Übersicht erscheint jetzt Stahl C35 mit den bekannten Werkstoffdaten. Den noch vorhanden Baustahl kann man löschen (Rechtsklick).
• Neben dem Material für die Stahlscheiben wird auch wieder das des Gummis benötigt. Damit die Simulationen konsistent bleiben, legen wir dieses selbst an:
  • Unter Stahl C35 wählt man dazu "Hier klicken, um ein neues Material hinzuzufügen"
  • Wir benennen das Material wieder als "Gummi-Nitril" (bestätigen mit <Enter>).
  • Aus der Toolbox am linken Rand fügt man jetzt Stück für Stück die relevanten Materialparameter zu den Eigenschaften des Gummis hinzu (Doppelklick oder Drag-and-Drop).
  • Für die mechanische Simulation ist die Linear-elastisch > Isotrope Elastizität (Isotropic Elasticity) nötig. (E-Modul = 12 N/mm², Poisson Zahl = 0,48)
  • Wenn man bewerten möchte, ob das Material unter Belastung versagt, sind die Parameter Festigkeit > Zugfestigkeit und Druckfestigkeit (Tensile Yield Strength, Compressive Yield Strength) notwendig. (Zugfestigkeit = 10 MPa, Druckfestigkeit = 110 MPa)
  • Zum Bewerten der Verformung durch das Eigengewicht ist die Physikalische Eigenschaften > Dichte (Density) anzugeben. (Dichte = 1,0 g/cm³)
  • Die thermische Simulation benötigt die Daten Physikalische Eigenschaften > Isotroper thermischer Sekanten-Ausdehnungskoeffizient (Isotropic Secant Coefficient of Thermal Expansion). (Expansionskoeff. therm. = 2,2E-4 1/K)
  • Hinweis: Allgemein ist die thermische Ausdehnung selbst von der Temperatur abhängig. Es gibt deshalb verschiedene Koeffizienten für Sekanten- und Tangentenmodul. Da wir ein einfaches Modell mit konstantem Parameter annehmen, ist die Unterscheidung für uns nicht von Bedeutung.
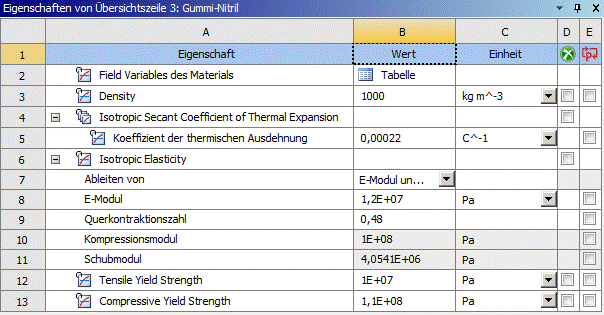
  • Die konkreten Zahlenwerte müssen konsistent zu denen in Fusion 360 gesetzt werden:

• Hinweis: In der aktuellen Version von Ansys Student kommt es scheinbar teilweise zu Fehlern bei der Spracheinstellung, weshalb an manchen Stellen die englischen Begriffe genutzt werden.

• Nachdem beide Materialien vollständig parametriert sind, kann man zur Projektübersicht zurückkehren.
• Die Geometrie lässt sich äquivalent zur ersten Übung über Kontextmenü > Geometrie importieren > Durchsuchen ... hinzufügen. Hier ist die zuvor gespeicherte Datei Gummipuffer_xx.step zu wählen.

Geometrie und Kontakte

Die weitere Konfiguration findet in GUI von Ansys Mechanical statt, die wir per Doppelklick auf Modell starten.

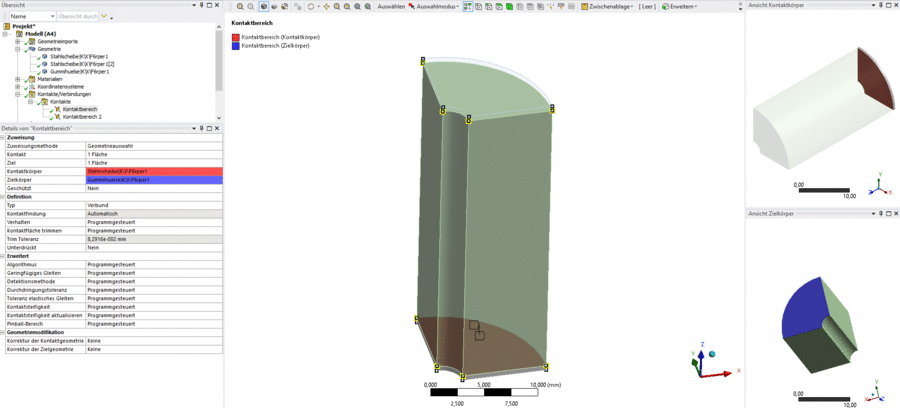
• In der 3D-Ansicht ist die aus Fusion 360 exportierte Geometrie zu sehen.
• Die einzelnen Körper tauchen mit den vergebenen Namen auch im Modellbaum auf.
• Im Gegensatz zur ersten Übung, ist den Körpern aber nicht automatisch ein Material zugewiesen worden. Das liegt daran, dass wir mehrere Parametersätze (Stahl und Gummi) definiert haben, und Ansys nicht zuordnen kann, zu welchem Körper welches Material gehört.
• Wir lösen die Fragezeichen vor den Geometrieelementen im Übersichtsbaum auf, indem wir jedem Körper in den jeweiligen Details von "..." das passende Material zuweisen.
• Bei Bedarf kann man über Details von "..." > Grafikeigenschaften > Farbe die Darstellung der einzelnen Körper anpassen.

Im nächsten Schritt müssen noch die Kontakte zwischen den Körpern definiert werden. Wird im Übersichtsbaum unter Projekt > Modell Kontakte/Verbindungen > Kontakte aufgeklappt, ist zu sehen, dass Ansys Mechanical bereits die zwei Kontakte zwischen dem Gummi und den Stahlscheiben erstellt hat. Die Kontaktflächen wurden korrekt zugewiesen. Das manuelle Anwählen von Geometrieelementen für Kontaktbereiche ist auch möglich und durch die Hilfsfenster mit Kontakt- und Zielkörper sehr komfortabel. Wir können uns diesen Schritt aber sparen.

Stattdessen sehen wir uns die Details von "Kontaktbereich" genauer an. Als Typ ist "Verbund" definiert. Das bedeutet, dass beide Teile fest miteinander verbunden sind. Die Knoten des einen Bauteils an der Kontaktfläche müssen also exakt den Bewegungen der Knoten des anderen Bauteils an der Kontaktfläche folgen. Die weiteren Optionen haben folgende Bedeutung:

• Keine Trennung: Hier dürfen die beiden Kontaktflächen aufeinander gleiten, können sich jedoch nicht lösen. Angewendet werden kann diese Option zum Beispiel für eine Achse in einem Gleitlager.
• Reibungsfrei: Hier ist auch ein reibungsfreies Gleiten möglich, jedoch können sich die Kontaktflächen oder Teile davon voneinander entfernen. Dies entspricht dem realistischen Verhalten zweier Körper, die aufeinanderstoßen können, ohne sich zu durchdringen. Ein Anwendungsbeispiel wäre das Ineinandergreifen von zwei (ideal) geschmierten Zahnrädern.
• Rau: Diese Option verhält sich wie die Option Reibungsfrei, jedoch haften die Kontakte hier stets. Statt eines Reibungskoeffizienten von 0 wird hier also ein Koeffizient von unendlich angenommen. Ein Beispiel wäre ein Autoreifen auf der Straße, wobei ein Schlupf ausgeschlossen wird.
• Reibungsbehaftet: Diese Option ist entsprechend eine Mischung aus Reibungsfrei und Rau und ist damit realistischer.

Während also die Option Verbund recht einfach implementiert werden kann, ist die Modellierung aller anderen Kontakttypen aufwändiger, da der Solver durch Abfragen der Position verschobener Knoten überprüfen muss, ob sich zwei Körper durchdringen würden oder nicht. Erst wenn dies der Fall ist, werden Kräfte auf die Knoten angetragen, um die entsprechende Durchdringung zu verhindern. In unserem Fall ist jedoch die "einfache" Option Verbund richtig.

Hintergrundinformationen zu Kontakten in FEM

Für das allgemeine Verständnis ist es an dieser Stelle sinnvoll, sich die Funktionsweise und Bedeutung von Kontaktstellen in FE-Modellen genauer klarzumachen. Da die Implementierung in Asnys dem Nutzer nicht sofort alle im Hintergrund ablaufenden Mechanismen deutlich macht, soll das Grundkonzept noch etwas ausführlicher betrachtet werden. Sobald man komplexere Kontaktprobleme als zwei "verklebte" Flächen betrachten möchte, ist dieses Wissen sehr hilfreich.

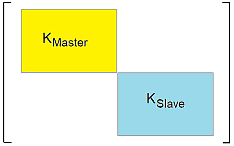
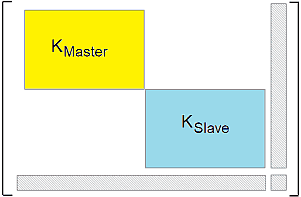
Nach dem Hinzufügen aller Bauteile zu einem FE-Modell existieren im Allgemeinen noch keine Wechselwirkungen zwischen Knoten ihrer Teilnetze (tritt im späteren Verlauf dieser Übung noch auf). Dies widerspiegelt sich in der Gesamt-Steifigkeitsmatrix der Baugruppe durch eine fehlende Überlappung zwischen den Bauteil-Steifigkeitsmatrizen (im Bild angedeutet für zwei Bauteile - allerdings bilden diese in der Realität keine geschlossenen Bereiche in der Matrix!).

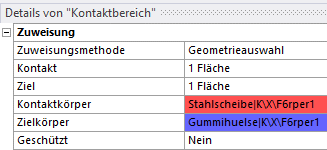
Bisher haben wir uns noch nicht um die korrekte Zuweisung der Master/Slave-Eigenschaft der Bauteile gekümmert (Bezeichnungen in Ansys: Kontakt und Ziel). Standardmäßig wurde die Stahlscheibe als Kontakt- und die Gummihülse als Zielkörper gekennzeichnet:

• Während der Simulation wird zwischen den Oberflächen der Master- und der Slave-Bauteile nach Kontaktzonen gesucht.
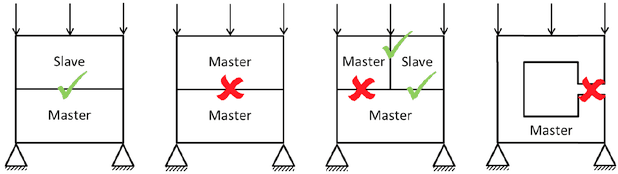
• Nur zwischen einem Master- und Slave-Bauteil ist eine Interaktion möglich. D.h. Kontakte zwischen Bauteilen gleicher Rolle (Master-Master bzw. Slave-Slave) können nicht abgebildet werden.
• Im Theoriehandbuch zum FEM-Programm Z88-Aurora (S.128) werden in einem Schema sehr anschaulich erlaubte und unzulässige Kontaktkonstellationen dargestellt.
• In Ansys ist die Definition von Kontakt/Master und Ziel/Slave aber nicht auf Körper beschränkt. Auch Flächen, Elemente und Knoten können angewählt werden. Damit sind auch Kontakte innerhalb eines Festkörpers möglich, wenn man dessen Oberflächen für die Zuweisung nutzt.

Ziel-Seite (target bzw. master):
stellt die Grenze des "zulässigen" Bewegungsbereiches dar (im Allgemeinen in Form der Element-Oberflächen).
Kontakt-Seite (contact bzw. slave):
wird der Ziel-Seite als Gegenseite zugeordnet (im allgemeinen die Knoten oder die Gaußpunkte).

Bei der Berechnung der Simulationsergebnisse wird in jeder Iteration geprüft, ob:

• die Kontakt-Seite im "zulässigen" Bewegungsbereich ist (mit Abstand von der Ziel-Seite → Kontakt ist "offen")
• oder im "unzulässigen" Bewegungsbereich (an Ziel-Seite anliegend oder in Ziel-Seite eingedrungen → Kontakt ist "geschlossen").

Entscheidungskriterien (nach Rangfolge geordnet), ob ein Bauteil "bewusst" zum Master deklariert werden sollte, sind folgende Eigenschaften im Rahmen der Baugruppe:

1. steiferer Körper
2. größere Ausdehnung der Kontaktfläche
3. schwächer gekrümmte Kontaktfläche
4. geringerer Diskretisierungsgrad
5. höherer Elementansatz

Die Stahlscheiben sind in unserer Baugruppe die steiferen Körper und die Kontaktflächen des Gummis ist nicht größer. Rein theoretisch wäre es also besser in der automatischen Kontaktdefinition von Ansys die Rollen von Ziel und Kontakt zu vertauschen. Unbedingt notwendig ist das in unserem recht einfachen Fall aber nicht.

Folgende weitere Eigenschaften können bei Kontaktproblemen neben dem Typ (siehe oben) von Interesse sein:

1. Erweitert > Pinball-Bereich
   • Dies ist der entscheidende Parameter für die Identifizierung der "möglichen" Kontaktzonen. Nur die Bereiche zweier Master/Slave-Bauteile, deren euklidischer Abstand unterhalb dieses Wertes liegt, werden als Kontaktzonen angesehen.
2. Erweitert > Detektionsmethode
   • Die Überwachung einer identifizierten Kontaktzone erfolgt nicht stetig über die kompletten Bereichsflächen, sondern über ein Raster von Stützstellen zwischen Master- und Slave-Bereich.
   • Standardmäßig werden die Gauß-Punkte zur Detektion genutzt.
   • Alternativ können Element-Knoten normal zum Kontakt oder Ziel ausgewertet werden.
3. Erweitert > Kontaktsteifigkeit
   • Im Kontaktbereich (bei geschlossenem Kontakt) wird eine sehr steife, elastische Zwischenschicht angenommen, welche die Kräfte zwischen den Kontaktflächen überträgt. Infolge ihrer großen Steifheit soll sie eine Durchdringung der Kontaktbereiche verhindern. Im Falle des verklebten Kontaktes soll sie auch ein Öffnen des Kontaktes unterbinden.
   • Für verklebte Kontakte werden üblicherweise gleiche Steifigkeitswerte in Normal- und Tangentialrichtung angenommen.
   • Für reibungsfreie Gleit-Kontakte kann man sich eine ideal gleitende Teflon-Schicht vorstellen, deren Steifigkeit in tangentialer Richtung Null ist.
   • Zu kleine Steifigkeitswerte führen bei der Simulation zu unzulässiger Durchdringung der Kontaktbereiche. Zu große Werte führen zu numerischen Problemen bei der Lösung des Gleichungssystems. Die optimalen Steifigkeitswerte sind sehr stark vom modellierten Problem abhängig. In der Praxis nimmt man eine kleine, aber praktisch vernachlässigbare Durchdringung der Kontaktbereiche in Kauf.
   • Der "Faktor"-Bezug auf die maximale Steifigkeit innerhalb des Modells erscheint als Einstieg am einfachsten, was sich auch in einem empfohlenem kleineren Wertebereich von ca. 1e3...1e5 widerspiegelt. D.h., die angenommene Kontakt-Zwischenschicht sollte einige 1000-mal steifer sein, als alle anderen Modellkomponenten.
   • Für "Absolut"-Werte der Steifigkeit ist der grob empfohlene Bereich mit 1e5...1e12 [N/mm] wesentlich größer, weil man dabei eigentlich die Steifigkeiten der Bauteile mit berücksichtigen muss.
4. Erweitert > Algorithmus
   • Hiermit wird das mathematische Verfahren definiert, mit dem die Kontaktbedingungen in das Gleichungssystem eingebaut werden.
   • In der Praxis haben sich zwei Methoden bewährt, um die Wirkung der Kontaktsteifigkeit im Modell nachzubilden → Penalty-Faktor und Lagrange-Multiplikator. Von der Lagrange-Methode existieren verschiedene Modifikationen zur Verbesserung der numerischen Stabilität.
   • "Pure Penalty"-Verfahren:
     • Jede Stützstelle des geschlossenen Kontaktes wird wie ein Feder-Element zwischen den Teilen des Modells simuliert. Bei Berührung am Kontakt werden für diese zusätzlichen Federn Element-Steifigkeitsmatrizen erstellt und dann als Beitrag in die Gesamt-Steifigkeitsmatrix eingefügt.
     • Ein Nachteil dieser Methode besteht darin, dass bei jeder Kontakt-Änderung eine Neubildung der Gesamt-Steifigkeitsmatrix erforderlich ist, welche Rechenzeit für deren Invertierung benötigt.
     • Ein Vorteil besteht darin, dass weniger Gleichgewichtsiterationen und eine schnelle Konvergenz zu erwarten sind.
   • "Augmented-Lagrange"-Verfahren:
     • Dieses Verfahren ermöglicht die Verknüpfung der ansonsten voneinander isolierten Bauteil-Steifigkeitsmatrizen innerhalb der Baugruppen-Steifigkeitsmatrix durch Einführen zusätzlicher Zeilen und Spalten. Die Anzahl dieser Zeilen und Spalten erhöht sich proportional zur Anzahl der möglichen Kontakt-Knoten:
       
     • Der geschlossene Kontakt wird aus physikalischer Sicht durch die entsprechenden Kontaktkräfte zwischen den Teilen des Modells simuliert. Bei Berührung am Kontakt werden dafür Anteile im Lastvektor eingefügt. Beim Übergang von offenem zu geschlossenem Kontakt müssen die Kräfte so bestimmt werden, dass nicht sofort bei der nächsten Iteration die Kontaktseiten "auseinander fliegen".
     • Die Gesamt-Steifigkeitsmatrix wird um die Kontaktbedingungen erweitert (ergibt größeres Gleichungssystem entsprechend der Anzahl zusätzlicher Zeilen und Spalten).
     • Ein Nachteil besteht darin, dass insbesondere beim Schalten von Kontakten das Verfahren zu numerischen Instabilitäten neigt. Damit sind mehr Gleichgewichtsiterationen notwendig, was dann zu einer relativ langsamen Konvergenz führt.
     • Ein Vorteil besteht darin, dass keine Neubildung der Gesamt-Steifigkeitsmatrix erforderlich ist und somit Rechenzeit eingespart wird. Es ergeben sich nur Beiträge im Lastvektor auf der rechten Seite des bestehenden Gleichungssystems und damit eine schnelle Lösung.
   • Die weiteren Methoden "MPC" und "Normal-Lagrange" sind hier dokumentiert.

Es gibt eine Vielzahl weiterer Optionen, die man sich bei Bedarf Stück für Stück über die Produktdokumentation erarbeiten kann.

Vernetzung

Beim Erstellen des FE-Netzes mit Standardeinstellungen entsteht ein gleichmäßiges Netz aus Hexaederelementen. Wir werden dieses lediglich durch Angabe zweier konkreter Elementgrößen verfeinern:
Elementgröße Stahlscheibe:

• Auswahl beider Körper mit der <Strg>-Taste
• Die gesamte Scheibe sollte mit 2 Elementschichten vernetzt werden, entsprechend ist der Wert der Elementgröße zu wählen.

Elementgröße Gummi:

• Auswahl des Gummikörpers und als Geometrie zuweisen
• Festlegen der Elementgröße auf die einfache Scheibendicke (Kompromiss aus Genauigkeit und Modellgröße)

Es sollte ein gleichmäßiges Netz mit ca. 95.000 Knoten und einer minimalen Elementqualität von etwa 0,5 entstehen. Diese Standardvernetzung ist dem Modell in Fusion 360 nach unserem bisherigen Wissen rein qualitativ schon überlegen und für die erste Studie ausreichend. Im späteren Verlauf der Übung werden wir trotzdem versuchen, die Qualität noch weiter zu erhöhen.

← →