Software: SimX - Einfuehrung - Elektro-Chaos - Schwingkreis mit C-Diode
Nach einigen theoretischen Betrachtungen, so im Folgenden versucht werden, reale physikalische Chaos-Experimente mittels der numerischen Simulation nachzuvollziehen. Dabei benutzen wir die Veröffentlichung Experimente zur Untersuchung linearer und nichtlinearer elektrischer Serienschwingkreise von Burkhard Wolf und Hans-Josef Patt, welche als PDF-Datei abrufbar ist.
Nichtlineare Systeme
Alle Systeme, welche keine linearen Systeme sind, sind nichtlineare Systeme:
- Nichtlineare Systeme enthalten Elemente, deren Parameterwerte abhängig von der Belastung des Elements sind (z.B. Kapazität als Funktion der anliegenden Spannung) oder erhalten "zufällige" Eingangssignale (z.B. Zeitabhängige Frequenzänderung der Betriebsspannung).
- Für nichtlineare Systeme existieren (im Normalfall) keine analytischen Lösungen.
- Nichtlinearität ist in Natur und Technik der Regelfall. Die linearen Näherungen der klassischen Natur- und Technikwissenschaften beschreiben nur die grundlegenden Effekte (=Zusammenhänge zwischen Ursache und Wirkung) der jeweiligen physikalisch-technischen Domäne (E-Technik, Mechanik, Fluidtechnik, usw.). Sie vermitteln damit das grundlegende Verständnis, welches man auch zur Modellierung nichtlinearer Systeme anwenden kann.
- Das Verhalten nichtlinearer Systeme kann der "gesunde Menschenverstand" nicht immer vorhersagen. Ähnliche Startbedingungen führen häufig zu stark verändertem Verhalten.
Chaotische Systeme
Damit ein nichtlineares System chaotisches Verhalten zeigt, müssen zusätzlich zur "Nichtlinearität" weitere Kriterien erfüllt sein:
- Es muss mindestens eine Stelle starker sensitiver Abhängigkeit von den Anfangsbedingungen existieren. Umgangssprachlich ist dies als Schmetterlingseffekt bekannt. Kleinste Änderungen der Startparameter führen langfristig zu völlig anderem Verhalten. Man spricht hierbei von deterministischem Chaos.
- Das System muss hinreichend viele Freiheitsgrade für die Bewegung im sogenannten Phasenraum besitzen:
- Der Zustand eines Systems wird zu jedem Zeitpunkt durch einen Punkt in einem Raum dargestellt werden, dessen Koordinatenachsen durch den Satz der unabhängigen Zustandsgrößen (meist die Integralgrößen) des Systems gegeben sind. Die Dynamik des Systems lässt sich damit als Bahn (Trajektorie) dieses Punktes im Phasenraum interpretieren. So wird beispielsweise der Phasenraum eines LCR-Schwingkreises durch den Spulenstrom und die Kondensatorspannung aufgespannt. Die ungedämpfte Schwingung entspricht einer geschlossenen Kurve um den Koordinatenursprung.
- Die Trajektorie eines Systems kann sich innerhalb des Phasenraums nicht schneiden, weil dies der Eindeutigkeit der Systementwicklung ausgehend von einem Punkt im Phasenraum widersprechen würde. In der Ebene kann es deshalb nur zu spiralähnlichen Kurven kommen. Als Spezialfall ist für ungedämpft oszillierende Systeme die geschlossene Trajektorie möglich.
- Erst durch einen zusätzlichen Freiheitsgrad ist es im Beispiel des LCR-Schwingkreises möglich, dass von der Spiralform abweichende Trajektorien entstehen, weil "Schnittpunkte" durch Ausweichen in der 3. Koordinatenachse vermieden werden können. Der zusätzliche Freiheitsgrad wird durch die frequenzveränderliche Anregung des Schwingkreises geschaffen.
Der Phasenraum eines Reihenschwingkreises
Ein LCR-Schwingkreis besitzt zwei Energiespeicher mit jeweils einer energetischen Zustandsgrößen (Spulenstrom und Kondensatorspannung):
- Der Wert einer energetischen Zustandsgröße beschreibt eindeutig die aktuell im zugehörigen Speicher enthaltene Energiemenge.
- Ausgehend von einem gegebenen Ladezustand der Energiespeicher entwickelt sich das System determiniert im Zeitbereich, weil zwischen den Speichern ein Energiefluss über die vorhandenen Verbindungselemente erfolgt.
- Die Entwicklung eines Systems in der Zeit wird durch die Werte aller Zustandsgrößen eindeutig beschrieben.
- Sehr anschaulich sieht man die Systementwicklung durch die Trajektorie der Zustandsgrößen im Phasenraum.
- Beim schrittweisen Aufbau des Chaos-Experiments werden wir den Phasenraum detailliert betrachten.
Linearer Schwingkreis
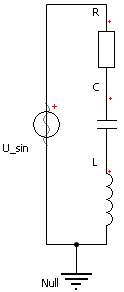
Wir beginnen mit dem Aufbau des Serienschwingkreises (Bild rechts) aus der durch einen Gyrator simulierten Spule (0,1...50 H), einem Drehkondensator (10..530 pF) und einem Serienwiderstand (50 Ω oder 1 kΩ). Laut Experimentieranleitung verwenden wir zuerst folgende Werte für die Bauelemente:
- C = 530 pF
- L = 10 H
- R = 1000 Ω
Wir beobachten mehrere Schwingungen ausgehend von einem auf 10 V aufgeladenen Kondensator:
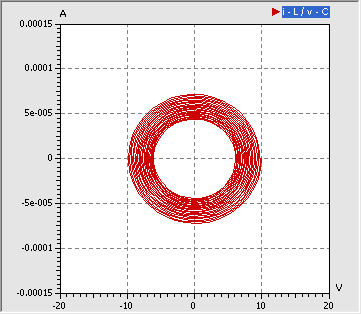
- Im Phasenraum widerspiegelt sich die durch den Serienwiderstand gedämpfte Schwingung als Spiral-Trajektorie in Richtung Koordinatenursprung [0,0]:
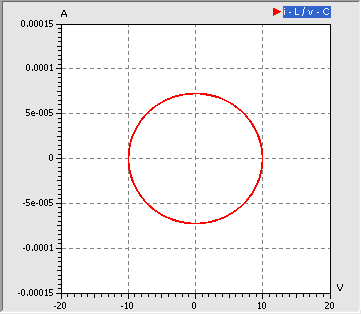
- Verringert man den Widerstand auf Null, so ergibt sich der Spezialfall der geschlossenen Trajektorie einer ungedämpften Schwingung:
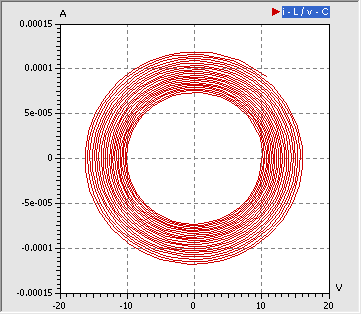
- Realisiert man den Serienwiderstand durch eine aktive elektronische Schaltung, so lassen sich auch negative ohmsche Widerstände realisieren. So können wir mit R=-1000 Ω die letzte mögliche Form der Trajektorie im zweidimensionalen Phasenraum beobachten - die sich ins Unendliche entwickelnde Spirale:
- Wir setzen den Serienwiderstand auf R=50 Ω. Damit ergibt sich eine nur leicht gedämpfte Schwingung.
Merke:
Die Trajektorie darf sich nicht kreuzen, ansonsten gäbe es ausgehend von einem Zustand mehr als eine weitere Entwicklungsmöglichkeit. Das ist in einem deterministischen System nicht möglich!
Fremderregter linearer Schwingkreis
Als Nächstes koppeln wir einen zeitabhängigen Frequenzgenerator an den Schwingkreis an (zur Ermittlung der Resonanzfrequenz):
- Der Kondensator erhält wieder die Anfangsspannung v0=0 V.
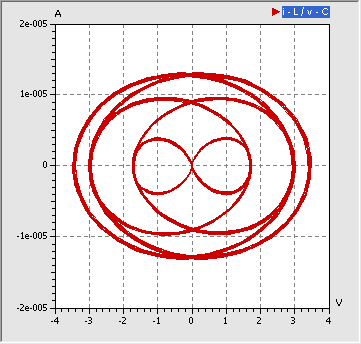
- Bei einem Zeitbereich von ca. 50 ms und einer festen Generatorfrequenz von 1400 Hz kann man im 2D-Phasendiagramm noch den Verlauf der Trajektorie erkennen:
Infolge der Fremderregung wird der Zustand des Gesamtsystems jetzt auch durch den aktuellen Wert der Betriebsspannung bestimmt. Es gibt also eine dritte Zustandsgröße, deren Koordinatenachse man sich im obigen Diagramm in der Tiefe vorstellen kann:
- Auch jetzt gibt es keine Kreuzungspunkte der Trajektorie. Wir sehen nur Kreuzungspunkte in der 2D-Projektion des Phasenraums, in Wirklichkeit verläuft die Trajektorie dort in unterschiedlichen Tiefen!
===>>> Hier geht es bald weiter !!!